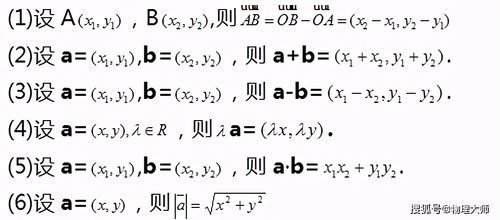如何理解和应用积化和差公式解决数学问题?
在数学的浩瀚星空中,隐藏着无数璀璨的宝石,它们或简单明了,引领初学者步入智慧殿堂;或深邃复杂,让探索者沉醉于思维的迷宫。今天,让我们一同揭开一颗既实用又迷人的宝石——积化和差公式的神秘面纱。这不是一场枯燥的理论宣讲,而是一场穿梭于数学奇境的奇妙旅行,让我们携手,用好奇与想象,为这段旅程增添无限色彩。
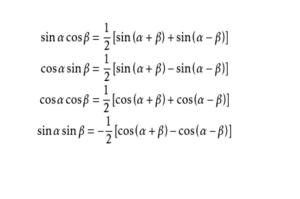
初探秘境:积与和的魔法转换
想象一下,你正站在一片由数字和公式构成的奇幻大陆上,四周是错综复杂的算式森林,而你手中握着一把名为“积化和差”的神奇钥匙。这把钥匙,能够解开那些看似互不相关的乘积表达式,将它们转化为更加友好、易于处理的和或差的形式。是不是很酷?

积化和差公式,简单来说,就是两个三角函数乘积的转化法则。它们像是数学界的魔术师,将原本难以直接求解的乘积问题,通过巧妙的变形,转化为利用已知三角函数性质就能轻松解决的和差问题。这不仅简化了计算过程,更揭示了三角函数之间深层次的联系和规律。
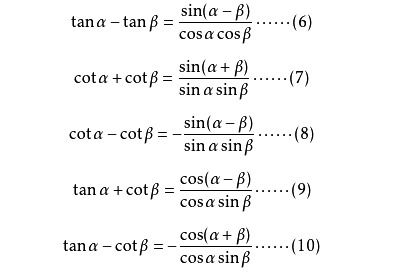
魔法揭秘:公式的奥秘
现在,让我们正式揭开积化和差公式的面纱。其实,这些公式并不复杂,它们基于三角函数的加法定理和基本的代数变换。以最基本的正弦和余弦函数的积化和差为例:
1. 正弦与正弦的积:
\[
\sin A \sin B = \frac{1}{2}[\cos(A-B) - \cos(A+B)]
\]
这个公式告诉我们,两个正弦函数的乘积可以转化为两个余弦函数的差的一半。想象一下,当两个正弦波相遇时,它们叠加产生的波形并非简单的乘积,但通过积化和差公式,我们可以将其视为两个余弦波(相位不同)的叠加效果。
2. 余弦与余弦的积:
\[
\cos A \cos B = \frac{1}{2}[\cos(A-B) + \cos(A+B)]
\]
同样地,两个余弦函数的乘积也可以转化为两个余弦函数的和的一半。这反映了余弦函数之间的和谐共生,它们在相互作用中展现出一种对称美。
3. 正弦与余弦的积(分为两种情况,这里以正弦在前为例):
\[
\sin A \cos B = \frac{1}{2}[\sin(A-B) + \sin(A+B)]
\]
这个公式揭示了正弦与余弦乘积的另一种表现形式,即两个正弦函数的和的一半。它告诉我们,正弦与余弦的乘积并非孤立无援,而是可以通过改变相位,转化为更为直观的和式。
应用之旅:从理论到实践的飞跃
掌握了这些公式,就像是获得了打开数学宝藏的钥匙。它们在实际问题中有着广泛的应用,尤其是在信号处理、物理计算、工程技术等领域。比如,在信号处理中,我们常常需要分析信号的频谱成分,而信号的频谱往往涉及到多个频率分量的叠加。利用积化和差公式,我们可以将复杂的乘积表达式转化为和差形式,从而更容易地识别出信号的各个频率分量。
此外,在解决某些复杂的三角恒等式证明、三角函数求值以及三角函数方程求解等问题时,积化和差公式也扮演着不可或缺的角色。它们就像是一位智慧的导师,引导我们绕过障碍,直达问题的核心。
思维的火花:超越公式的思考
然而,积化和差公式的魅力远不止于此。它们不仅仅是数学工具,更是思维的火花,激发我们对数学之美的深刻感悟。通过这些公式,我们可以看到数学中的统一与和谐,感受到不同数学概念之间的紧密联系。它们教会我们,数学并非冷冰冰的公式堆砌,而是充满了生命力和创造力的学科。
在探索积化和差公式的过程中,我们学会了如何运用已知条件去推导未知结果,如何通过变换视角来解决问题。这些思维方法不仅在数学中至关重要,在日常生活和工作中也同样适用。它们让我们变得更加灵活和富有创造力,能够更好地应对各种挑战和变化。
结语:数学之旅,未完待续
就这样,我们结束了对积化和差公式的奇妙探索。但请记住,这仅仅是数学之旅的一个小小片段。在数学的海洋中,还有无数未知的领域等待我们去发现、去征服。让我们带着对数学的热爱和敬畏之心,继续前行吧!在未来的日子里,或许我们还会遇到更多像积化和差公式这样神奇而美妙的数学宝藏。让我们一起期待那些未知而精彩的瞬间吧!
- 上一篇: 轻松几步,网上购泰山门票全攻略
- 下一篇: 等价无穷小公式是什么?初学者如何理解和应用这些公式?
-
 揭秘积化和差公式的奇妙变换新闻资讯12-02
揭秘积化和差公式的奇妙变换新闻资讯12-02 -
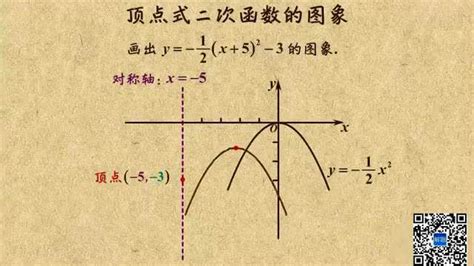 一元二次方程顶点坐标公式是什么,怎么求?新闻资讯11-13
一元二次方程顶点坐标公式是什么,怎么求?新闻资讯11-13 -
 如何区分减数、被减数和差?新闻资讯01-12
如何区分减数、被减数和差?新闻资讯01-12 -
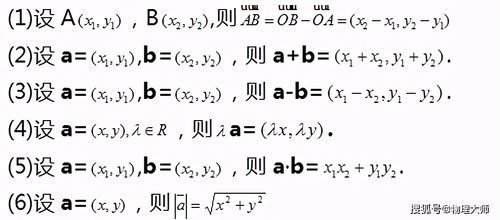 向量平行与垂直的公式是什么?新闻资讯11-05
向量平行与垂直的公式是什么?新闻资讯11-05 -
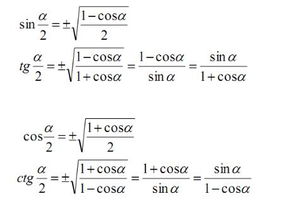 详解半角公式与二倍角公式的定义与应用新闻资讯10-18
详解半角公式与二倍角公式的定义与应用新闻资讯10-18 -
 等价无穷小公式是什么?初学者如何理解和应用这些公式?新闻资讯12-22
等价无穷小公式是什么?初学者如何理解和应用这些公式?新闻资讯12-22