详解半角公式与二倍角公式的定义与应用
在数学的广阔天地里,三角函数作为连接几何与代数的桥梁,扮演着举足轻重的角色。而半角公式与二倍角公式,作为三角函数变换中的基本且重要的工具,不仅在理论研究上占据一席之地,更在实际问题解决中展现出其独特的魅力。本文将深入浅出地介绍这两类公式,帮助读者全面理解其内涵、推导过程及应用场景。
一、引言
三角函数,如正弦(sin)、余弦(cos)、正切(tan)等,描述了直角三角形中边与角之间的关系,进而扩展到任意角度的度量。在解决周期性现象、波形分析、天体运动等众多领域时,三角函数都展现出了强大的应用能力。半角公式与二倍角公式,作为三角函数变换技巧的一部分,能够让我们在已知某些三角函数值的基础上,快速求解其他角度或形式的三角函数值,极大地简化了计算过程。

二、二倍角公式
2.1 定义与形式
二倍角公式是指利用一个角的三角函数值来表示其两倍角的三角函数值的公式。对于任意角α,其正弦、余弦、正切的二倍角公式分别为:

正弦二倍角公式:$\sin 2\alpha = 2\sin\alpha\cos\alpha$
余弦二倍角公式:$\cos 2\alpha = \cos^2\alpha - \sin^2\alpha$(或等价地,$\cos 2\alpha = 2\cos^2\alpha - 1 = 1 - 2\sin^2\alpha$)
正切二倍角公式:$\tan 2\alpha = \frac{2\tan\alpha}{1 - \tan^2\alpha}$(注意,此公式在$\tan\alpha \neq 1$时成立)
2.2 推导简述
正弦二倍角公式的推导通常利用正弦和余弦的和差公式,即$\sin(A+B) = \sin A\cos B + \cos A\sin B$,令$A=B=\alpha$即可得到。余弦二倍角公式则可通过余弦的平方与正弦平方和为1的性质推导,或直接从正弦二倍角公式和同角三角函数关系得出。正切二倍角公式则基于正弦、余弦的二倍角公式以及正切的定义进行推导。
2.3 应用实例
二倍角公式在求解三角方程、化简三角函数表达式、进行三角恒等变换等方面有着广泛的应用。例如,在求解$\cos 45^\circ$时,可以利用余弦二倍角公式,先求出$\cos 90^\circ = 0$(作为已知),然后通过$\cos 45^\circ = \pm \sqrt{\frac{1+\cos 90^\circ}{2}}$(取正值)得到$\cos 45^\circ = \frac{\sqrt{2}}{2}$。
三、半角公式
3.1 定义与形式
半角公式,顾名思义,是用来表示一个角的一半的三角函数值与该角三角函数值之间关系的公式。对于任意角α(其中α/2不在特殊角如终边在坐标轴上等特殊情况),其正弦、余弦、正切的半角公式分别为:
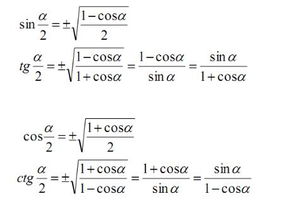
正弦半角公式:$\sin\frac{\alpha}{2} = \pm \sqrt{\frac{1 - \cos\alpha}{2}}$(取正负号依据α/2所在象限)
余弦半角公式:$\cos\frac{\alpha}{2} = \pm \sqrt{\frac{1 + \cos\alpha}{2}}$(同样取正负号依据α/2所在象限)
正切半角公式:$\tan\frac{\alpha}{2} = \frac{1 - \cos\alpha}{\sin\alpha} = \frac{\sin\alpha}{1 + \cos\alpha}$(注意,分母不能为0)
3.2 推导简述
正弦、余弦半角公式的推导常利用同角三角函数的基本关系(如$\sin^2\theta + \cos^2\theta = 1$)和余弦的二倍角公式进行。通过适当的代数变换,可以得到上述半角公式的形式。正切半角公式则可以通过正弦、余弦的半角公式及正切的定义直接推导得出。
3.3 应用实例
半角公式在解决与角度减半相关的问题时非常有用,如计算一个锐角的半角的正弦、余弦或正切值,或者在证明某些三角恒等式中发挥作用。例如,已知$\cos\alpha = \frac{3}{5}$(且α为锐角),求$\sin\frac{\alpha}{2}$的值。
-
 高中数学半角公式大全及应用方法全面求解新闻资讯10-21
高中数学半角公式大全及应用方法全面求解新闻资讯10-21 -
 椭圆的标准公式详解新闻资讯11-07
椭圆的标准公式详解新闻资讯11-07 -
 椭圆周长计算公式详解新闻资讯11-24
椭圆周长计算公式详解新闻资讯11-24 -
 转速与角速度转换公式详解新闻资讯11-06
转速与角速度转换公式详解新闻资讯11-06 -
 轻松掌握:log函数求导公式详解新闻资讯11-09
轻松掌握:log函数求导公式详解新闻资讯11-09 -
 数学标准差计算公式的详解新闻资讯10-25
数学标准差计算公式的详解新闻资讯10-25












