椭圆的标准公式详解
在探讨几何学的奇妙世界时,椭圆作为一个基础而重要的形状,其独特的性质和多样的公式无疑是学习与研究中的重点内容。椭圆不仅广泛存在于自然界中,如行星轨道、天体运动路径,还在工程设计、建筑设计等领域发挥着不可或缺的作用。为了深入理解椭圆,掌握其相关公式显得尤为重要。本文将详细介绍椭圆的定义、标准方程、焦点性质、长短轴关系、面积公式、周长近似公式以及与其他几何形状的关系,通过丰富的关键词和详尽的解释,帮助读者更好地掌握椭圆的公式及其应用。
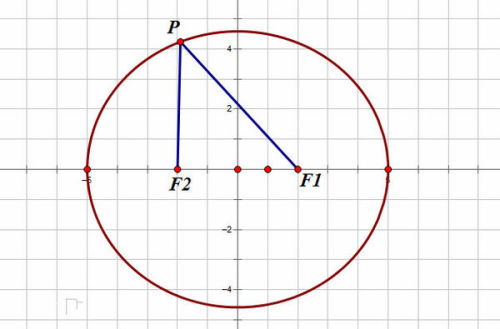
椭圆的定义是理解其所有公式的基础。椭圆可以定义为平面上到两个定点(焦点)的距离之和等于常数(且大于两定点之间的距离)的点的轨迹。这两个定点被称为椭圆的焦点,而常数则等于椭圆的长轴长。基于这一定义,可以推导出椭圆的标准方程。在直角坐标系中,若椭圆的长轴和短轴分别与x轴和y轴平行,则椭圆的标准方程可以表示为x^2/a^2+y^2/b^2=1,其中a为长轴半径,b为短轴半径,且a>b。若椭圆的长轴和短轴不平行于坐标轴,则可通过旋转坐标系或利用一般二次曲线的性质进行求解。

椭圆的焦点性质是其几何特征的重要体现。根据椭圆的定义,可以推导出焦距c的公式,即c^2=a^2-b^2。这一公式揭示了椭圆长轴、短轴与焦距之间的内在关系。同时,焦点在椭圆上的位置也具有对称性,即椭圆关于其长轴和短轴都是对称的,且焦点位于长轴的两侧,距离长轴中心各为c。这一性质在解决椭圆相关的几何问题时具有重要作用。

长短轴关系是研究椭圆形态的基础。在椭圆的标准方程中,长轴和短轴的长度分别由a和b表示。根据椭圆的定义和性质,可以知道a和b的大小关系决定了椭圆的形状。当a远大于b时,椭圆呈现出扁平的形态;当a和b相差不大时,椭圆则接近圆形。通过调整a和b的值,可以生成不同形态的椭圆,从而满足各种实际应用的需求。
面积公式是计算椭圆大小的关键。椭圆的面积可以通过公式S=πab计算得出,其中a为长轴半径,b为短轴半径。这一公式简洁明了,易于应用,是计算椭圆面积的首选方法。在工程设计、建筑设计等领域,常常需要计算椭圆面积以确定所需材料的数量或空间的布局。因此,掌握椭圆面积公式对于提高工作效率和准确性具有重要意义。
周长近似公式则是解决椭圆周长计算难题的有效途径。由于椭圆周长的精确公式较为复杂且难以实际应用,因此通常采用近似公式进行估算。常见的椭圆周长近似公式包括拉马努金公式、拉姆伯特公式等。这些公式通过数学推导和实验验证得出,具有较高的准确性和适用性。在需要计算椭圆周长的场合,可以根据具体情况选择合适的近似公式进行计算。
此外,椭圆还与其他几何形状具有密切的联系。例如,椭圆可以看作是圆在平面上的拉伸或压缩变形;椭圆与双曲线、抛物线等二次曲线在性质和公式上具有一定的相似性;椭圆还可以通过投影、旋转等操作转化为其他几何形状。这些联系不仅丰富了椭圆的理论内容,还为解决复杂几何问题提供了更多的思路和方法。
在椭圆的应用方面,其独特的性质和多样的公式使其在各个领域具有广泛的应用价值。在物理学中,椭圆轨道是行星、卫星等天体运动的重要特征之一;在工程学中,椭圆形状被广泛应用于传动机构、压力容器等部件的设计中;在美术学和建筑学中,椭圆则常被用作构图元素和装饰图案以营造出优雅和谐的美感效果。
综上所述,椭圆的公式是理解其性质和应用的基础。通过掌握椭圆的标准方程、焦点性质、长短轴关系、面积公式、周长近似公式以及与其他几何形状的关系等知识点,可以更加深入地了解椭圆的奥秘和魅力。同时,这些公式和知识点也为解决实际问题提供了有力的数学工具和支持。在未来的学习和工作中,我们应该继续深化对椭圆及其相关公式的理解和掌握程度,以更好地应对各种挑战和机遇。
在进一步的学习和研究过程中,我们可以尝试将椭圆的公式应用于实际问题中进行分析和计算。例如,在工程设计领域,可以利用椭圆面积公式计算某一椭圆形区域的面积以确定所需材料的数量;在物理学领域,可以运用椭圆轨道公式分析行星的运动轨迹和速度等参数;在美术学和建筑学领域,则可以运用椭圆的几何性质进行构图设计和装饰图案的创作等。通过这些实践应用活动,我们可以更加深入地理解椭圆的公式和性质,并将其转化为解决实际问题的能力和智慧。
总之,椭圆的公式是几何学中的重要内容之一。通过学习和掌握这些公式及其相关知识点,我们可以更加全面地了解椭圆的性质和应用价值。同时,这些公式也为解决实际问题提供了有力的数学支持和实践指导。在未来的学习和工作中,我们应该继续加强对椭圆及其相关公式的理解和掌握程度,以不断提升自己的数学素养和综合能力水平。
- 上一篇: 《阅微草堂笔记》的精准译文解析
- 下一篇: 250在爱情中的寓意是什么
-
 椭圆周长计算公式详解新闻资讯11-24
椭圆周长计算公式详解新闻资讯11-24 -
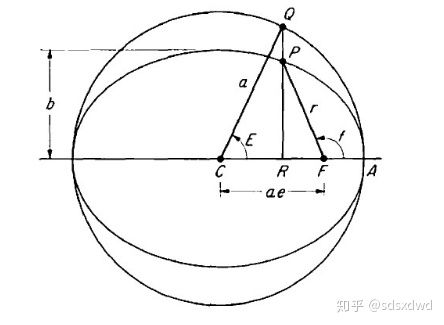 揭秘:椭圆面积公式全解析新闻资讯11-25
揭秘:椭圆面积公式全解析新闻资讯11-25 -
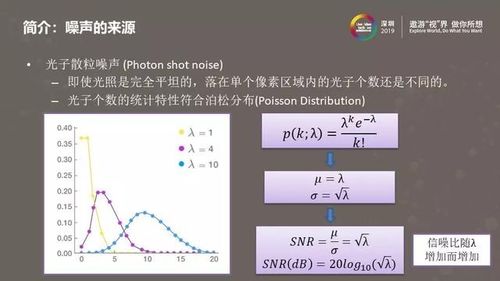 数学标准差计算公式的详解新闻资讯10-25
数学标准差计算公式的详解新闻资讯10-25 -
 揭秘!椭圆面积公式的计算方法,轻松掌握新闻资讯10-21
揭秘!椭圆面积公式的计算方法,轻松掌握新闻资讯10-21 -
 真空度计算公式详解,轻松掌握计算方法!新闻资讯11-12
真空度计算公式详解,轻松掌握计算方法!新闻资讯11-12 -
 转速与角速度转换公式详解新闻资讯11-06
转速与角速度转换公式详解新闻资讯11-06









