揭秘:椭圆面积公式全解析
椭圆的面积公式是椭圆几何学中一个至关重要的概念,它不仅在数学上有着广泛的应用,还在物理学、工程学等领域发挥着重要作用。椭圆作为一种特殊的平面曲线,其面积的计算方法具有独特的数学美感。以下将详细探讨椭圆的面积公式及其推导过程,并通过实例展示其应用。
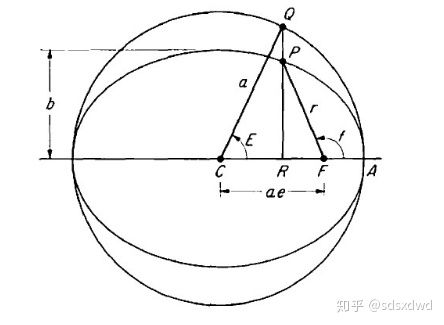
椭圆是一种平面内到两个定点(焦点)的距离之和等于常数的点的轨迹。这两个定点(焦点)位于椭圆的长轴上,且到椭圆上任意一点的距离之和等于椭圆的长轴长。椭圆的形状由两个参数决定:长轴半径a和短轴半径b,其中a>b。在直角坐标系中,椭圆的标准方程可以表示为:

\[

\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1
\]
(当焦点在x轴上时);或
\[
\frac{y^2}{a^2} + \frac{x^2}{b^2} = 1
\]
(当焦点在y轴上时)。
椭圆的面积公式为:
\[
S = \pi ab
\]
这个公式表明,椭圆的面积等于长轴半径a与短轴半径b的乘积再乘以π。下面我们将详细推导这个公式。
椭圆面积公式的推导
推导椭圆面积公式的一种常见方法是利用定积分。首先,我们考虑椭圆在第一象限的部分,其方程可以表示为:
\[
y = b\sqrt{1 - \left(\frac{x}{a}\right)^2}
\]
(其中0≤x≤a)。
椭圆在第一象限的面积可以表示为:
\[
S_1 = \int_0^a b\sqrt{1 - \left(\frac{x}{a}\right)^2} \, dx
\]
为了简化这个积分,我们可以进行换元。令:
\[
x = a\sin\theta \quad (\text{其中} \, 0 \leq \theta \leq \frac{\pi}{2})
\]
则:
\[
dx = a\cos\theta \, d\theta
\]
将x和dx代入原积分中,得到:
\[
S_1 = \int_0^{\frac{\pi}{2}} b\sqrt{1 - \left(\frac{a\sin\theta}{a}\right)^2} \cdot a\cos\theta \, d\theta
\]
\[
= \int_0^{\frac{\pi}{2}} b\sqrt{1 - \sin^2\theta} \cdot a\cos\theta \, d\theta
\]
\[
= \int_0^{\frac{\pi}{2}} b\cos\theta \cdot a\cos\theta \, d\theta
\]
\[
= ab \int_0^{\frac{\pi}{2}} \cos^2\theta \, d\theta
\]
接下来,我们利用三角恒等式:
\[
\cos^2\theta = \frac{1 + \cos2\theta}{2}
\]
代入上式,得到:
\[
S_1 = ab \int_0^{\frac{\pi}{2}} \frac{1 + \cos2\theta}{2} \, d\theta
\]
\[
= \frac{ab}{2} \int_0^{\frac{\pi}{2}} (1 + \cos2\theta) \, d\theta
\]
\[
= \frac{ab}{2} \left[ \theta + \frac{1}{2}\sin2\theta \right]_0^{\frac{\pi}{2}}
\]
\[
= \frac{ab}{2} \left( \frac{\pi}{2} + 0 - 0 - 0 \right)
\]
\[
= \frac{\pi ab}{4}
\]
由于椭圆关于x轴和y轴都是对称的,所以整个椭圆的面积是四个第一象限部分面积的和,即:
\[
S = 4S_1 = 4 \cdot \frac{\pi ab}{4} = \pi ab
\]
这就得到了椭圆的面积公式。
椭圆面积公式的应用
椭圆面积公式在实际问题中有着广泛的应用。以下是一些常见的应用场景:
1. 物理学中的应用:在物理学中,椭圆轨道是行星绕恒星运动的一种常见轨迹。通过椭圆面积公式,我们可以计算出行星在某一时间段内扫过的椭圆面积,从而进一步分析其运动规律。
2. 工程学中的应用:在工程设计中,椭圆形状常用于各种结构件的设计。例如,椭圆形的管道、椭圆形的梁等。通过椭圆面积公式,我们可以方便地计算出这些结构件的面积,从而进行进一步的设计和优化。
3. 地理学中的应用:在地理学中,椭圆形状也常用于描述一些自然现象。例如,地球的形状可以近似看作是一个椭球体。通过椭圆面积公式,我们可以计算出地球表面的某些区域面积,这对于气候研究、地质勘探等领域具有重要意义。
4. 艺术和设计中的应用:在艺术和设计领域,椭圆形状也经常被用于各种设计元素中。例如,椭圆形的窗户、椭圆形的装饰图案等。通过椭圆面积公式,我们可以计算出这些设计元素的面积,从而确保它们在整体设计中的比例和协调性。
结论
综上所述,椭圆的面积公式是椭圆几何学中一个非常重要的概念。它不仅在数学上有着广泛的应用,还在物理学、工程学、地理学以及艺术和设计等领域发挥着重要作用。通过推导椭圆面积公式的过程,我们可以更深入地理解椭圆的性质和应用。同时,利用椭圆面积公式,我们可以方便地计算出各种椭圆形状的面积,从而为实际问题的解决提供有力的数学工具。
- 上一篇: 揭秘!吴邪隐藏的惊人真实身份
- 下一篇: 掌握“not only...but also”的绝妙用法
-
 揭秘!椭圆面积公式的计算方法,轻松掌握新闻资讯10-21
揭秘!椭圆面积公式的计算方法,轻松掌握新闻资讯10-21 -
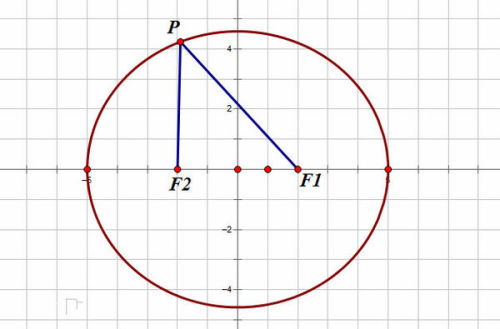 椭圆的标准公式详解新闻资讯11-07
椭圆的标准公式详解新闻资讯11-07 -
 问答揭秘:椭圆面积怎么求?一步一步教你搞定!新闻资讯10-21
问答揭秘:椭圆面积怎么求?一步一步教你搞定!新闻资讯10-21 -
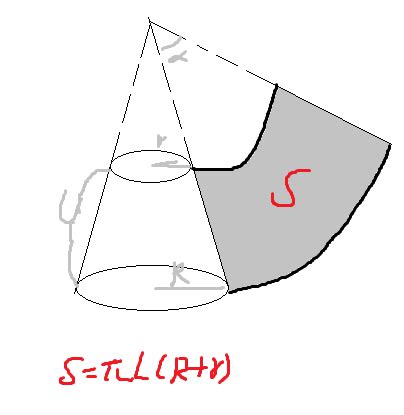 揭秘!圆台侧面积计算公式大公开,你了解多少?新闻资讯10-25
揭秘!圆台侧面积计算公式大公开,你了解多少?新闻资讯10-25 -
 揭秘:概率计算公式全解析新闻资讯10-25
揭秘:概率计算公式全解析新闻资讯10-25 -
 揭秘!直角三角形面积计算的神奇公式新闻资讯10-30
揭秘!直角三角形面积计算的神奇公式新闻资讯10-30