揭秘!椭圆面积公式的计算方法,轻松掌握
在探索数学的广袤宇宙中,椭圆这一几何形态以其独特的魅力吸引着无数学者与爱好者的目光。作为平面内到两个定点(焦点)的距离之和等于常数的动点轨迹,椭圆不仅在日常生活中随处可见,如行星绕日轨道、光学仪器设计乃至建筑设计等领域,都扮演着重要角色。而椭圆的面积公式,作为理解其几何特性与计算其空间占据量的基础,更是连接理论与实践的桥梁。本文将从多个维度深入剖析椭圆的面积公式,带您领略这一数学之美的全貌。

一、椭圆的定义与基本性质
首先,让我们从椭圆的定义出发。椭圆可以描述为平面上所有到两个固定点(称为焦点)距离之和等于常数(且大于两焦点之间的距离)的点的集合。这两个固定点,即焦点,是椭圆形成的关键。椭圆的中心称为中心点或椭圆心,通常与坐标原点重合或通过平移可与之重合。

椭圆具有一系列基本性质,包括:其对称性(关于长轴、短轴及两条对角线均对称)、焦点性质(任意一点到两焦点的距离之和为常数)、长短轴(长轴为穿过椭圆中心且过两个顶点的线段,短轴则垂直于长轴并过椭圆的另外两个顶点)等。这些性质为我们后续推导面积公式提供了坚实的理论基础。
二、面积公式的历史渊源
椭圆的面积公式并非一蹴而就,其推导过程蕴含了人类智慧的结晶。早在古希腊时期,数学家们就开始了对椭圆的研究,但直到17世纪,随着微积分学的兴起,椭圆的面积公式才得到了精确的表示。特别是牛顿和莱布尼茨在微积分领域的开创性工作,为求解复杂图形的面积问题提供了强有力的工具。
三、面积公式的推导过程
1. 积分法推导
现代数学中,最常用的椭圆面积公式推导方法之一是利用微积分中的定积分。设椭圆的标准方程为$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$(其中$a>b>0$),我们可以将其改写为$y = b\sqrt{1 - \frac{x^2}{a^2}}$(仅考虑上半部分,因为椭圆关于x轴对称,故总面积需乘以2)。然后,利用定积分计算由椭圆曲线、x轴和两条垂直于x轴的直线(分别位于椭圆的左右顶点处)围成的图形的面积,即
$$S = 2 \int_{-a}^{a} b\sqrt{1 - \frac{x^2}{a^2}} \, dx$$
通过换元法或三角代换等技巧,可以进一步求解该积分,最终得到椭圆面积的精确表达式:
$$S = \pi ab$$
2. 几何法启示
除了微积分方法外,历史上也曾有数学家尝试通过几何构造来直观理解椭圆的面积。虽然这种方法可能不如微积分严谨,但它提供了另一种思考角度,有助于我们更直观地感受椭圆的几何美。例如,通过考虑椭圆与一系列平行线或圆的相交情况,结合割补法等几何技巧,可以间接地“感知”到椭圆面积与长轴、短轴乘积之间的关系。
四、面积公式的应用与意义
椭圆的面积公式不仅在纯数学领域具有重要地位,它在众多实际应用中也发挥着关键作用。
物理学:在物理学中,天体运动的研究经常涉及椭圆轨道。通过计算椭圆的面积,可以进一步分析行星运动的周期、速度等参数,为天文学研究提供重要依据。
工程学:在工程设计领域,如桥梁、隧道等结构的截面设计,有时会采用椭圆形以提高结构的稳定性和美观性。此时,椭圆面积的计算就显得尤为重要。
经济学:在经济学领域,虽然直接应用椭圆面积公式的场景不多,但椭圆作为一种优化模型,在资源分配、成本最小化等问题中,其面积的最大化或最小化往往代表着效率或效益的最优解。
五、结语
综上所述,椭圆的面积公式不仅是数学领域的一个重要定理,更是连接理论与实践的桥梁。从定义与性质的探讨,到历史渊源的追溯,再到推导过程的详细剖析,最后到其在多个领域的广泛应用,我们不难发现,这一简单的公式背后蕴含着丰富的数学思想和广泛的应用前景。它不仅是人类智慧的结晶,更是我们探索未知、改造世界的有力工具。在未来的学习与研究中,让我们继续以敬畏之心,探索更多数学之美,让智慧之光照亮前行的道路。
- 上一篇: 日字旁加成字念什么?
- 下一篇: 香港回归辉煌瞬间:1997年那一刻,月与日的历史铭记!
-
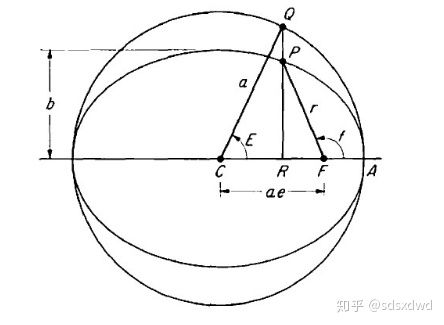 揭秘:椭圆面积公式全解析新闻资讯11-25
揭秘:椭圆面积公式全解析新闻资讯11-25 -
 椭圆面积的计算方法新闻资讯10-31
椭圆面积的计算方法新闻资讯10-31 -
 揭秘梯形面积计算的奥秘:一键掌握高效公式新闻资讯12-22
揭秘梯形面积计算的奥秘:一键掌握高效公式新闻资讯12-22 -
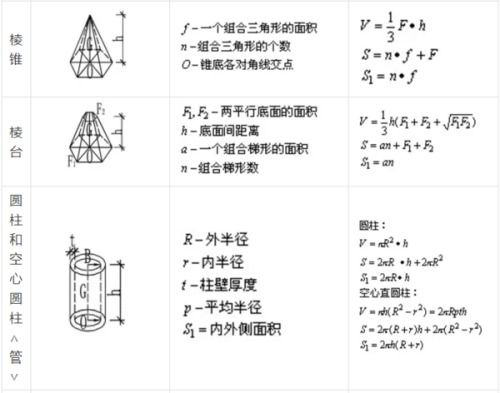 揭秘!圆锥表面积的神奇计算公式,一看就懂!新闻资讯11-01
揭秘!圆锥表面积的神奇计算公式,一看就懂!新闻资讯11-01 -
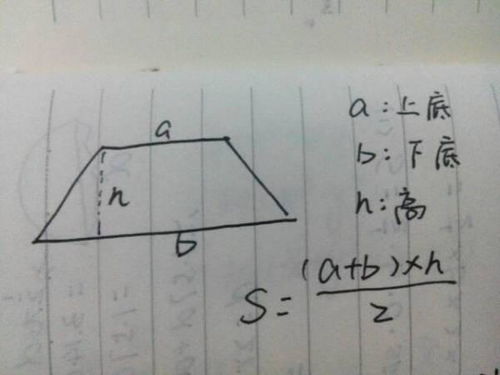 揭秘!梯形面积公式的字母魅力:轻松掌握计算奥秘新闻资讯10-24
揭秘!梯形面积公式的字母魅力:轻松掌握计算奥秘新闻资讯10-24 -
 揭秘!扇形面积的三大计算公式,你掌握了吗?新闻资讯10-27
揭秘!扇形面积的三大计算公式,你掌握了吗?新闻资讯10-27












