揭秘梯形面积计算的奥秘：一键掌握高效公式

在日常生活和数学学习中，我们经常会遇到各种形状的面积计算问题，其中梯形作为一种常见的四边形，其面积的计算方法既实用又有趣。想象一下，当你需要测量一块不规则田地中梯形部分的面积，以便合理规划种植时，掌握梯形面积公式就显得尤为重要了。那么，接下来，我们就来一场轻松愉快的探索之旅，深入了解梯形面积公式的奥秘。

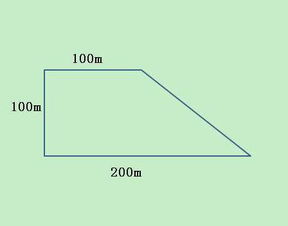
梯形：一个不平凡的四边形

首先，让我们从认识梯形开始。梯形，顾名思义，就是一组对边平行而不相等的四边形。它有两条平行的边，我们称之为上底和下底，而另外两条边则是斜边，连接着上底和下底的两个端点。这种独特的结构赋予了梯形独特的性质和计算方法。

梯形面积公式的诞生

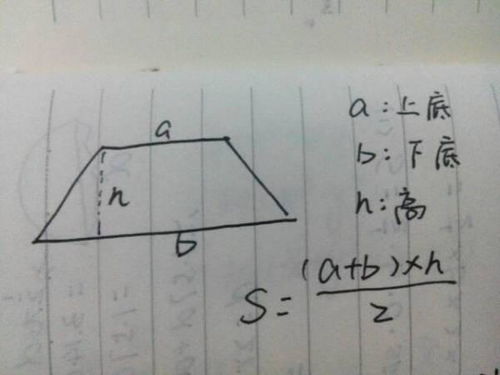
要计算梯形的面积，数学家们经过长期的观察和实践，总结出了一个简单而高效的公式。这个公式就像一把钥匙，解锁了梯形面积计算的秘密。梯形面积公式是：

$$ \text{面积} = \frac{(a + b) \times h}{2} $$

其中，$a$ 代表上底的长度，$b$ 代表下底的长度，而 $h$ 则是梯形的高，即从上底到下底的垂直距离。

公式背后的逻辑

这个公式看起来简单，但它背后蕴含着深刻的数学原理。我们可以这样理解：首先，想象一下如果我们能把梯形变成一个矩形，那么面积的计算就会变得非常简单，直接就是长乘以宽。但梯形不是矩形，怎么办呢？

一个巧妙的方法是，我们可以在梯形内部“补”上一个与梯形完全相同但方向相反的梯形，这样它们组合起来就形成了一个平行四边形。而这个平行四边形的“长”就是梯形上底和下底之和的一半，即 $\frac{a + b}{2}$，高仍然是 $h$。平行四边形的面积计算公式是底乘以高，所以整个平行四边形的面积是 $\frac{a + b}{2} \times h$。因为我们是用两个梯形拼成了一个平行四边形，所以单个梯形的面积就是这个面积的一半，即 $\frac{(a + b) \times h}{2}$。

如何应用梯形面积公式

了解了梯形面积公式的由来和逻辑后，接下来我们看看如何在实际生活中应用它。

场景一：家居装修

假设你正在为家中的一面梯形墙面选购壁纸，首先你需要知道这块墙面的面积。测量出上底、下底和高之后，代入梯形面积公式，就能轻松得到所需壁纸的面积了。

场景二：农业规划

在农业领域，梯形地块非常常见。为了合理安排作物种植，你需要知道每块梯形地块的面积。同样地，通过测量上底、下底和高，使用梯形面积公式，你就能得到精确的面积数据。

场景三：建筑设计

在建筑设计中，梯形元素也经常被运用到屋顶、楼梯等设计中。设计师需要准确计算这些梯形部分的面积，以确保材料的合理使用和成本的精确控制。梯形面积公式在这里同样发挥着重要作用。

注意事项

在使用梯形面积公式时，有几点需要注意：

1. 准确测量：上底、下底和高的测量必须准确，否则会影响面积计算的精确度。

2. 单位统一：在进行计算时，确保所有长度单位（如米、厘米等）保持一致，避免单位换算带来的误差。

3. 理解公式：不要仅仅死记硬背公式，要理解其背后的逻辑和推导过程，这样才能灵活运用。

结语

通过上面的介绍，相信你已经对梯形面积公式有了深入的了解。这个看似简单的公式，不仅在数学领域有着广泛的应用，更在日常生活和工作中发挥着不可替代的作用。掌握它，不仅能让你的数学学习更加得心应手，还能让你的生活更加便捷和高效。下次当你遇到梯形面积的计算问题时，不妨试试用梯形面积公式来解决吧！