梯形体积的奥秘:轻松掌握计算方法
梯形体积的计算是几何学中的一个重要问题,尤其在工程学、建筑设计以及物理学等领域中,经常需要用到梯形体积的计算方法。本文将详细介绍梯形体积的计算方法,并通过实例来演示如何应用这些方法来解决实际问题。

首先,我们需要明确梯形的定义。梯形是一组对边平行但长度不相等的四边形。当梯形被用作三维形状(如棱柱)的底面时,其体积的计算就变得复杂一些。为了简化问题,我们通常考虑一种特殊情况,即梯形棱柱的体积计算。梯形棱柱是指底面为梯形、顶面与底面平行且相等、侧面为矩形的三维形状。

梯形体积的计算公式可以通过将梯形棱柱分解为若干个小的矩形或平行六面体来推导。这种方法称为微积分法,其基本思想是将复杂形状分解为简单的几何形状,然后对这些简单形状进行积分。然而,对于梯形棱柱这种特殊情况,我们可以采用一种更简单的方法来计算其体积,即利用梯形面积和高度来计算。

梯形面积的计算公式为:面积 = (上底 + 下底) × 高 ÷ 2。这个公式是通过将梯形分解为两个三角形和一个矩形(或平行四边形)来推导的。其中,上底和下底是梯形的两个平行边的长度,高是它们之间的距离。

一旦我们知道了梯形的面积,就可以通过乘以梯形棱柱的高度来计算其体积。梯形棱柱的体积公式为:体积 = 梯形面积 × 高度。这里的“高度”是指梯形棱柱的高,即从底面到顶面的垂直距离。
现在,让我们通过一个具体的例子来演示如何计算梯形棱柱的体积。假设我们有一个梯形棱柱,其底面是一个梯形,上底长度为5厘米,下底长度为10厘米,高(梯形的垂直高度)为6厘米;而梯形棱柱的高(从底面到顶面的垂直距离)为12厘米。
首先,我们计算梯形的面积。根据梯形面积的计算公式:
面积 = (5厘米 + 10厘米) × 6厘米 ÷ 2 = 15厘米 × 6厘米 ÷ 2 = 90厘米² ÷ 2 = 45厘米²
然后,我们将梯形的面积乘以梯形棱柱的高度来计算其体积:
体积 = 45厘米² × 12厘米 = 540厘米³
所以,这个梯形棱柱的体积是540立方厘米。
除了梯形棱柱之外,梯形体积的计算还可能涉及其他形状,如梯形锥体(底面为梯形、顶点在底面外的锥体)。梯形锥体的体积计算稍微复杂一些,因为我们需要考虑锥体的几何特性。梯形锥体的体积公式可以通过将梯形锥体分解为若干个小的平行六面体或利用微积分的方法推导出来。然而,对于大多数实际应用来说,我们可以采用一种近似的方法来计算梯形锥体的体积,即使用梯形面积乘以锥体的高度,然后再除以3(这是锥体体积的一般公式:体积 = 底面积 × 高度 ÷ 3)。
假设我们有一个梯形锥体,其底面是一个梯形,上底长度为4厘米,下底长度为8厘米,高(梯形的垂直高度)为5厘米;而锥体的高度(从底面到顶点的垂直距离)为10厘米。我们可以先计算梯形的面积,然后再利用梯形锥体的体积公式来计算其体积。
梯形的面积为:
面积 = (4厘米 + 8厘米) × 5厘米 ÷ 2 = 12厘米 × 5厘米 ÷ 2 = 60厘米² ÷ 2 = 30厘米²
梯形锥体的体积为:
体积 = 30厘米² × 10厘米 ÷ 3 = 300厘米³ ÷ 3 = 100厘米³
所以,这个梯形锥体的体积是100立方厘米。
需要注意的是,虽然这种方法对于大多数实际应用来说是足够的,但在某些精度要求较高的场合下,可能需要采用更精确的计算方法。例如,可以利用微积分中的三重积分或数值方法来计算复杂形状的体积。这些方法虽然更复杂一些,但能够提供更高的精度和更广泛的应用范围。
另外,梯形体积的计算还可能受到其他因素的影响,如梯形的倾斜角度、侧面的形状和大小等。在实际应用中,我们需要根据具体情况来选择合适的计算方法和参数。
总之,梯形体积的计算是几何学中的一个重要问题,涉及多种形状和计算方法。通过掌握梯形面积和高度等基本几何量以及相关的计算公式和原理,我们可以有效地解决梯形体积的计算问题,并将其应用于各种实际场合中。
此外,对于需要更高精度或更复杂形状的梯形体积计算问题,我们可以考虑采用更先进的计算方法和技术手段来解决。随着计算机科学和数值方法的不断发展,我们可以利用计算机软件和算法来模拟和计算复杂形状的体积,为工程设计和科学研究提供更加精确和可靠的数据支持。同时,我们也需要不断学习和掌握新的几何知识和计算方法,以适应不断变化的应用需求和挑战。
- 上一篇: 温馨的同义词
- 下一篇: 揭秘:轻松查找电子版结婚证的实用方法
-
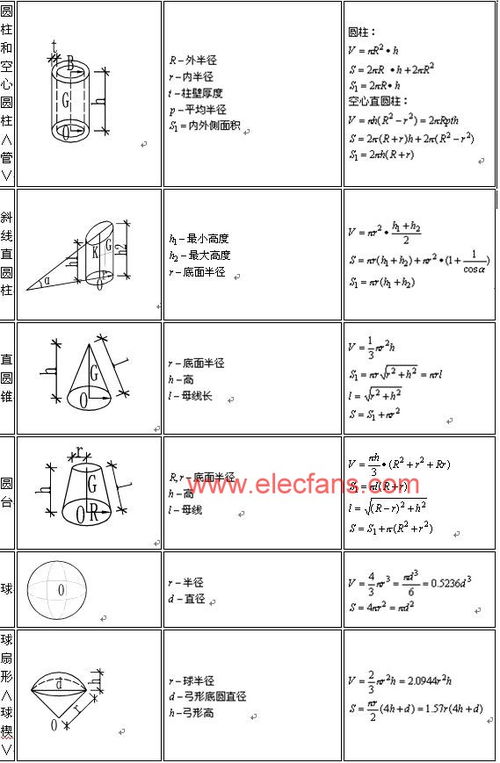 梯形体积该如何计算?新闻资讯11-12
梯形体积该如何计算?新闻资讯11-12 -
 揭秘梯形面积计算的奥秘:一键掌握高效公式新闻资讯12-22
揭秘梯形面积计算的奥秘:一键掌握高效公式新闻资讯12-22 -
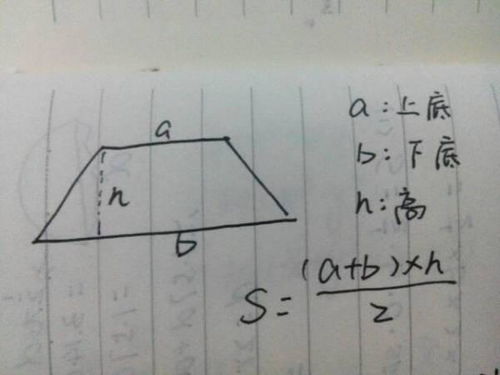 揭秘!梯形面积公式的字母魅力:轻松掌握计算奥秘新闻资讯10-24
揭秘!梯形面积公式的字母魅力:轻松掌握计算奥秘新闻资讯10-24 -
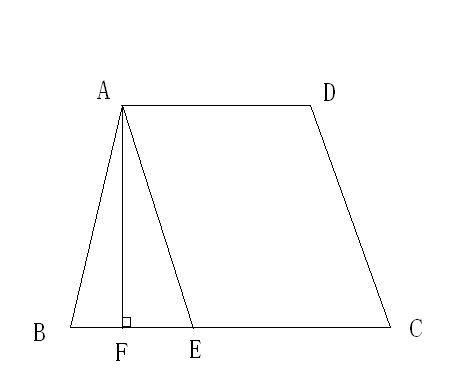 揭秘梯形面积计算的奥秘新闻资讯10-30
揭秘梯形面积计算的奥秘新闻资讯10-30 -
 揭秘梯形面积计算的奥秘公式新闻资讯10-30
揭秘梯形面积计算的奥秘公式新闻资讯10-30 -
 揭秘!圆柱体积计算的神奇公式,轻松掌握空间奥秘新闻资讯10-19
揭秘!圆柱体积计算的神奇公式,轻松掌握空间奥秘新闻资讯10-19











