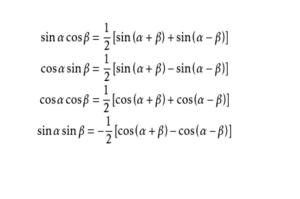揭秘积化和差公式的奇妙变换
探索数学之美:揭秘积化和差公式的奥秘

在数学的世界里,隐藏着许多令人惊叹的规律和公式,它们如同璀璨的星辰,点缀着人类智慧的夜空。其中,积化和差公式便是一颗耀眼的明珠,它以其独特的魅力和广泛的应用,吸引着无数数学爱好者去探索、去领悟。今天,就让我们一起走进积化和差公式的世界,感受它所带来的数学之美。

一、初识积化和差公式

积化和差公式,是三角函数恒等变换中的一类重要公式。它揭示了两个三角函数的乘积与它们的和差之间的关系,为我们在解决三角函数问题时提供了一种全新的视角和方法。具体来说,积化和差公式包括正弦、余弦、正切等多种形式的变换,其中最基本的是正弦和余弦的积化和差公式。

正弦的积化和差公式为:
sinαcosβ = [sin(α+β) + sin(α-β)] / 2
余弦的积化和差公式为:
cosαcosβ = [cos(α+β) + cos(α-β)] / 2
以及它们的变种形式,如正弦与正弦的积化和差、余弦与正弦的积化和差等。这些公式看似简单,却蕴含着深刻的数学原理,是三角函数变换中的基础工具。
二、积化和差公式的推导
积化和差公式的推导过程,既是对三角函数性质的深入探索,也是对数学思维的锻炼和提升。以下以正弦的积化和差公式为例,简要介绍其推导过程。
首先,我们知道正弦函数的和差公式为:
sin(α+β) = sinαcosβ + cosαsinβ
sin(α-β) = sinαcosβ - cosαsinβ
将这两个公式相加,得到:
sin(α+β) + sin(α-β) = 2sinαcosβ
移项后,即可得到正弦的积化和差公式:
sinαcosβ = [sin(α+β) + sin(α-β)] / 2
同样地,我们可以利用余弦函数的和差公式推导出余弦的积化和差公式。这一过程不仅加深了我们对三角函数性质的理解,也锻炼了我们的逻辑推理能力和数学运算能力。
三、积化和差公式的应用
积化和差公式在三角函数问题中的应用广泛而深入。它不仅可以用于化简三角函数表达式,还可以用于求解三角函数方程、证明三角函数恒等式等。以下列举几个典型的应用场景:
1. 化简三角函数表达式
在解决三角函数问题时,我们经常会遇到复杂的三角函数表达式。利用积化和差公式,我们可以将这些复杂的表达式化简为更简单的形式,从而更容易地求出结果。例如,在求解某些三角函数的最值问题时,我们可以利用积化和差公式将表达式化简为关于单一角度的三角函数形式,进而利用三角函数的性质求出最值。
2. 求解三角函数方程
在求解三角函数方程时,我们有时会遇到形如sinαcosβ = C(C为常数)的方程。这时,我们可以利用积化和差公式将方程转化为关于α和β的和差形式的三角函数方程,从而更容易地求出α和β的值。这种方法在求解某些复杂的三角函数方程时尤为有效。
3. 证明三角函数恒等式
三角函数恒等式是数学中的一类重要等式,它们揭示了三角函数之间的内在联系。在证明三角函数恒等式时,我们经常会用到积化和差公式。通过巧妙地运用积化和差公式,我们可以将复杂的恒等式转化为更简单的形式,从而更容易地证明其正确性。
四、积化和差公式的启示
积化和差公式不仅在数学领域有着广泛的应用,还给我们带来了深刻的启示。它告诉我们,在数学中,许多看似复杂的问题都可以通过巧妙的变换和转化变得简单明了。这种思想和方法不仅适用于三角函数问题,还可以推广到更广泛的数学领域甚至其他学科中。
首先,积化和差公式教会我们要善于观察和发现数学中的规律和模式。在解决数学问题时,我们应该善于观察问题的结构和特点,寻找其中隐藏的规律和模式,从而找到解决问题的关键。
其次,积化和差公式还告诉我们,要善于运用已有的知识和方法去解决新的问题。在数学中,许多新的问题都可以通过已有的知识和方法得到解决。因此,我们应该注重基础知识的积累和学习方法的掌握,以便在遇到新问题时能够迅速找到解决问题的方法。
最后,积化和差公式还启示我们要勇于探索和创新。在数学中,许多新的发现和成果都是通过探索和创新得到的。因此,我们应该勇于尝试新的思路和方法,不断挑战自己的极限,以取得更大的成就。
五、结语
积化和差公式是数学中的一颗璀璨明珠,它以其独特的魅力和广泛的应用吸引着无数数学爱好者去探索、去领悟。通过学习和掌握积化和差公式,我们不仅可以提高解决三角函数问题的能力,还可以培养自己的数学思维和创新能力。让我们在数学的世界里继续前行,不断探索和发现更多的数学之美吧!
- 上一篇: 如何轻松关闭拼多多的先用后付功能?
- 下一篇: 移动硬盘损坏后数据能否恢复?
-
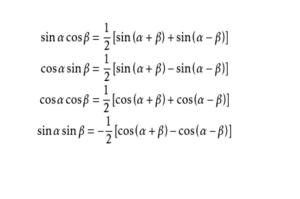 如何理解和应用积化和差公式解决数学问题?新闻资讯12-22
如何理解和应用积化和差公式解决数学问题?新闻资讯12-22 -
 揭秘对数函数Log的基石:掌握这些基本公式,解锁数学新视界!新闻资讯10-25
揭秘对数函数Log的基石:掌握这些基本公式,解锁数学新视界!新闻资讯10-25 -
 如何区分减数、被减数和差?新闻资讯01-12
如何区分减数、被减数和差?新闻资讯01-12 -
 揭秘!四边形面积计算公式的全攻略新闻资讯11-01
揭秘!四边形面积计算公式的全攻略新闻资讯11-01 -
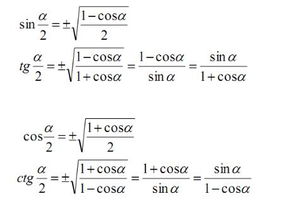 详解半角公式与二倍角公式的定义与应用新闻资讯10-18
详解半角公式与二倍角公式的定义与应用新闻资讯10-18 -
 揭秘:频率公式的定义与应用,你不可不知的实用知识!新闻资讯11-01
揭秘:频率公式的定义与应用,你不可不知的实用知识!新闻资讯11-01