如何区分减数、被减数和差?
在数学的基础运算中,减法是一个至关重要的概念。当我们谈论减法时,不可避免地会遇到三个核心概念:减数、被减数和差。对于初学者而言,理解并区分这三个概念可能存在一定的难度。本文旨在清晰、简洁地介绍这三个概念,并通过实例加深理解,帮助读者更好地掌握减法运算。

首先,我们来明确这三个概念的定义。在减法运算中,被减数通常是减法算式中的第一个数,也就是减号“-”前面的那个数。它代表了起始的总量或者我们想要从中减去一部分数量的那个数值。减数则是减法算式中的第二个数,即减号“-”后面的那个数。它表示我们需要从被减数中去掉的数量。最后,差是减法运算的结果,也就是被减数减去减数后所得的数值。它反映了减法操作之后剩余的数量。

为了更好地理解这三个概念,我们可以将减法运算视为一个“减法故事”。在这个故事中,被减数就像是一个装满水果的篮子,减数是我们想要从中拿走的水果数量,而差则是最终篮子里剩下的水果数量。例如,在算式“10 - 3 = 7”中,10就是被减数,它代表了初始时篮子里的水果总数;3是减数,表示我们从篮子里拿走了三个水果;而7则是差,即最后篮子里剩下的水果数量。
接下来,我们进一步探讨这三个概念在实际问题中的应用。在日常生活中,我们经常需要用到减法来解决各种问题。例如,在购物时,我们需要从预算中减去购买商品的价格,以确定剩余的金额。在这个过程中,预算就相当于被减数,购买的商品价格则是减数,而剩余的金额就是差。同样地,在库存管理、财务管理、时间规划等领域,减法运算也扮演着重要的角色。
此外,我们还可以通过图形化的方式来帮助理解这三个概念。在数轴上,被减数可以表示为一个点,减数可以表示为从该点向左移动的距离,而差则表示移动后的新位置。这种图形化的表示方法不仅有助于直观地理解减法运算的过程,还能帮助我们更好地掌握负数、绝对值等进阶概念。
值得注意的是,虽然被减数、减数和差在减法运算中扮演着不同的角色,但它们之间并不是孤立的。在实际问题中,我们需要根据具体情况来确定哪个数是被减数,哪个数是减数,以及它们的值是多少。有时,同一个问题可能可以用不同的方式来建立减法算式,但这并不会改变最终的差。例如,在算式“15 - 8 = 7”和“8 + ? = 15”中,虽然它们的形式不同,但实质上都涉及到相同的被减数(15)、减数(8)和差(7)。这种灵活性使得减法运算在解决实际问题时具有更广泛的应用。
当然,在学习减法运算的过程中,我们还需要注意一些常见的错误和误区。例如,有些初学者可能会混淆被减数和减数的位置,导致计算结果错误。为了避免这种错误,我们可以采用一些记忆技巧,如将被减数想象成“大的那个数”,将减数想象成“小的那个数”(尽管这并不总是准确的,但在大多数情况下可以帮助我们快速区分它们)。此外,我们还可以通过多做练习来加深对这三个概念的理解和运用。
最后,我们强调一下这三个概念在数学教育中的重要性。被减数、减数和差不仅是减法运算的基础概念,也是后续学习其他数学概念(如方程、不等式、函数等)的重要基础。因此,在学习这些概念时,我们需要给予足够的重视和关注。通过深入理解这些概念的本质和内涵,我们可以更好地掌握减法运算的技巧和方法,为后续的数学学习打下坚实的基础。
综上所述,被减数、减数和差是减法运算中的三个核心概念。它们分别代表了减法算式中的起始数量、去掉的数量和剩余的数量。通过明确这三个概念的定义和内涵,并结合实际问题进行应用和分析,我们可以更好地掌握减法运算的技巧和方法。同时,我们还需要注意避免一些常见的错误和误区,通过多做练习来加深对这三个概念的理解和记忆。只有这样,我们才能在数学学习中不断取得进步和成就。
- 上一篇: 如何操作使用西瓜影音
- 下一篇: 微信号修改全攻略:轻松几步,让你的微信ID焕然一新
-
 问答揭秘:如何轻松区分减数与被减数?新闻资讯10-23
问答揭秘:如何轻松区分减数与被减数?新闻资讯10-23 -
 Excel技巧:一键生成减法算术题新闻资讯04-01
Excel技巧:一键生成减法算术题新闻资讯04-01 -
 揭秘积化和差公式的奇妙变换新闻资讯12-02
揭秘积化和差公式的奇妙变换新闻资讯12-02 -
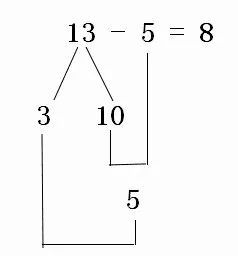 小学一年级数学下册如何运用破十法进行计算?新闻资讯10-23
小学一年级数学下册如何运用破十法进行计算?新闻资讯10-23 -
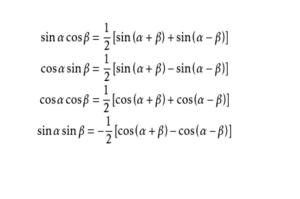 如何理解和应用积化和差公式解决数学问题?新闻资讯12-22
如何理解和应用积化和差公式解决数学问题?新闻资讯12-22 -
 高效教学:掌握破十法的实用步骤与技巧新闻资讯10-23
高效教学:掌握破十法的实用步骤与技巧新闻资讯10-23