等价无穷小公式是什么?初学者如何理解和应用这些公式?
等价无穷小公式:简化极限计算的强大工具
在微积分学这一严谨而精妙的数学领域中,等价无穷小公式是求解极限问题的一把利器。它不仅能够简化计算过程,还能提升解题效率,使得原本复杂的极限问题变得直观易懂。本文将深入浅出地介绍等价无穷小公式的定义、应用、注意事项及拓展,旨在为读者提供一个全面而清晰的理解框架。

一、等价无穷小的定义
等价无穷小,顾名思义,是指两个无穷小量在某一自变量趋近过程中表现出等价性。具体来说,当两个函数$f(x)$和$g(x)$在自变量$x$趋近于某个值(通常为0)时,如果它们的极限值相等,即$\lim_{{x \to a}} \frac{f(x)}{g(x)} = 1$,则称$f(x)$和$g(x)$在$x$趋近于$a$时是等价无穷小,记作$f(x) \sim g(x)$。

这一概念的核心在于两个无穷小量趋向于零的速度相同,或者说,在极限运算中,它们可以相互替换而不影响最终结果。

二、等价无穷小公式大全
在微积分的学习中,掌握一些基本的等价无穷小公式至关重要。以下是几组常用的等价无穷小关系:

1. 三角函数类
当$x \to 0$时,$\sin x \sim x$,$\tan x \sim x$,$\arcsin x \sim x$,$\arctan x \sim x$。
这些公式在处理含有三角函数的极限问题时尤为有用,能够将复杂的三角函数转化为简单的线性函数。
2. 指数与对数类
当$x \to 0$时,$e^x - 1 \sim x$,$\ln(1+x) \sim x$。
这类公式在处理指数函数和对数函数的极限时,能够显著简化计算步骤。
3. 幂函数类
当$x \to 0$时,$(1+x)^n - 1 \sim nx$。
该公式在幂函数极限的计算中发挥着重要作用,特别是在处理形如$(1+x)^n$的表达式时。
4. 其他常用公式
当$x \to 0$时,$1 - \cos x \sim \frac{1}{2}x^2$,$a^x - 1 \sim x\ln a$($a > 0, a \neq 1$)。
这些公式在处理特定类型的极限问题时,能够提供更为便捷的求解路径。
三、等价无穷小公式的应用
等价无穷小公式在微积分中的应用广泛,主要包括但不限于以下几个方面:
1. 简化极限计算
在求解极限问题时,如果直接计算较为复杂,可以尝试将表达式中的部分项替换为等价的无穷小量,从而简化计算过程。例如,计算$\lim_{{x \to 0}} \frac{\sin x}{x}$时,可直接利用$\sin x \sim x$进行替换,得到$\lim_{{x \to 0}} \frac{x}{x} = 1$。
2. 求导数和积分
在求导数和积分的过程中,有时会遇到难以直接处理的表达式。此时,可以利用等价无穷小公式进行近似替换,从而简化计算。虽然这种方法可能会引入一定的误差,但在许多情况下,这种误差是可以接受的。
3. 分析函数性质
等价无穷小公式还可以用于分析函数的性质,如单调性、极值等。通过将函数在特定点附近进行等价无穷小替换,可以更容易地判断函数的性质。
四、等价无穷小替换的注意事项
尽管等价无穷小公式在微积分中具有强大的应用价值,但在使用过程中仍需注意以下几点:
1. 适用范围
等价无穷小公式只适用于自变量趋近于某一值(通常为0)的情况。在其他情况下,直接使用这些公式可能会导致错误的结果。
2. 保持关系不变
在应用等价无穷小替换时,需要确保替换前后的无穷小量具有相同的极限性质和变化趋势。否则,替换可能会导致计算错误。
3. 结合其他方法
对于一些复杂的极限问题,等价无穷小公式可能无法直接应用。此时,需要结合其他方法(如洛必达法则、泰勒公式等)进行求解。
4. 注意精度要求
在使用等价无穷小公式进行近似计算时,需要注意精度要求。如果精度要求较高,则可能需要采用更精确的方法进行计算。
五、等价无穷小公式的拓展
除了上述基本的等价无穷
- 上一篇: 如何理解和应用积化和差公式解决数学问题?
- 下一篇: 请问'card'这个词具体是什么意思?
-
 无穷小量等价代换的常用公式是什么?新闻资讯12-22
无穷小量等价代换的常用公式是什么?新闻资讯12-22 -
 arctanx(反正切函数)的表达式或等价公式是什么?新闻资讯12-22
arctanx(反正切函数)的表达式或等价公式是什么?新闻资讯12-22 -
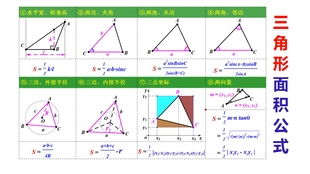 三角形面积计算公式详解新闻资讯11-25
三角形面积计算公式详解新闻资讯11-25 -
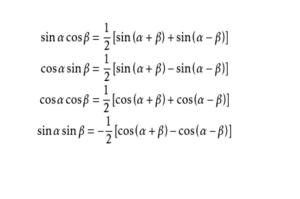 如何理解和应用积化和差公式解决数学问题?新闻资讯12-22
如何理解和应用积化和差公式解决数学问题?新闻资讯12-22 -
 相遇问题常用的六大公式是什么?新闻资讯11-07
相遇问题常用的六大公式是什么?新闻资讯11-07 -
 三角形面积的计算公式是什么?新闻资讯11-10
三角形面积的计算公式是什么?新闻资讯11-10