相遇问题常用的六大公式是什么?
相遇问题六大公式详解

在解决相遇问题时,我们需要掌握和理解一些基本的公式和概念。相遇问题通常涉及两个或多个物体在特定条件下相遇的情况,这些条件可能包括速度、时间、距离等。以下是相遇问题的六大核心公式,以及它们的应用和推导过程。

一、基本相遇公式
公式一:总路程 = 甲的路程 + 乙的路程
这是相遇问题中最基本的公式。当两个物体从两地同时出发,相向而行,它们在某一点相遇时,它们各自走过的路程之和等于两地之间的总路程。
例如,甲从A地出发,乙从B地出发,相向而行,在C点相遇。那么,甲从A到C的路程加上乙从B到C的路程就等于A、B两地之间的总路程。
二、速度和公式
公式二:速度和 = 甲的速度 + 乙的速度
在相遇问题中,如果两个物体相向而行,那么它们的相对速度就是它们各自速度的和。这是因为它们都在朝着对方移动,所以它们的速度会叠加。
例如,甲的速度是5米/秒,乙的速度是3米/秒,它们相向而行。那么,它们的相对速度就是5米/秒 + 3米/秒 = 8米/秒。
三、相遇时间公式
公式三:相遇时间 = 总路程 ÷ 速度和
这个公式用于计算两个物体相遇所需的时间。根据公式二,我们知道两个物体相向而行的相对速度是它们速度的和。因此,相遇时间就是总路程除以相对速度。
例如,A、B两地相距1000米,甲的速度是5米/秒,乙的速度是3米/秒。它们相向而行,那么相遇时间就是1000米 ÷ (5米/秒 + 3米/秒) = 125秒。
四、各自路程公式
公式四:甲的路程 = 甲的速度 × 相遇时间
公式五:乙的路程 = 乙的速度 × 相遇时间
这两个公式用于计算相遇时各自走过的路程。根据相遇时间公式,我们可以求出相遇时间,然后分别用甲、乙的速度乘以相遇时间,就可以得到它们各自走过的路程。
例如,在上面的例子中,我们已经求出相遇时间是125秒。那么,甲的路程就是5米/秒 × 125秒 = 625米,乙的路程就是3米/秒 × 125秒 = 375米。
五、环形跑道相遇公式
公式六:相遇次数 = 总路程 ÷ 跑道长度 × 相遇时间(跑道长度为两人速度差的最小公倍数时)
这个公式用于解决环形跑道上的相遇问题。在环形跑道上,两个物体同向而行,它们会在某个点相遇。但是,由于跑道是环形的,所以它们相遇的次数不仅与速度和时间有关,还与跑道的长度有关。
当两个物体的速度差是跑道长度的整数倍时,它们会在每次跑完这个整数倍的跑道长度时相遇。因此,相遇次数就是总路程除以跑道长度再乘以相遇时间(这里的相遇时间是指它们跑完整数倍跑道长度所需的时间)。但是,更常见的情况是,我们直接通过设定未知数(如相遇时的圈数)和列方程来求解环形跑道上的相遇问题。
例如,甲、乙两人在400米的环形跑道上同向而行,甲的速度是6米/秒,乙的速度是4米/秒。他们何时会相遇?
我们可以设相遇时甲跑了x圈,那么乙就跑了x-1圈(因为甲要追上乙才能相遇,所以甲跑的圈数要比乙多一圈)。那么,甲跑的总路程就是400x米,乙跑的总路程就是400(x-1)米。
由于他们的速度差是2米/秒,所以他们相遇时所用的时间就是他们跑的总路程之差除以速度差,即[400x - 400(x-1)] ÷ 2 = 200秒。
但是,如果我们用公式六来求解,就会比较复杂。因为在这个问题中,跑道长度400米并不是他们速度差2米/秒的最小公倍数。所以,我们不能直接用总路程除以跑道长度再乘以相遇时间来求解相遇次数。但是,我们可以知道,他们每次相遇时,甲都会比乙多跑一圈。因此,我们可以通过设定未知数(如相遇时的圈数)和列方程来求解。
六、公式应用实例
以下是一个综合应用上述公式的实例:
甲、乙两车分别从A、B两地同时出发,相向而行。甲车的速度是60千米/小时,乙车的速度是40千米/小时。A、B两地相距300千米。求两车
- 上一篇: 越剧是在哪个省形成的地方剧种?
- 下一篇: 儿童溜冰初学者入门指南
-
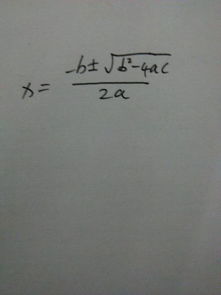 揭秘!数学达人必知的六大解方程黄金公式,轻松化解难题!新闻资讯10-28
揭秘!数学达人必知的六大解方程黄金公式,轻松化解难题!新闻资讯10-28 -
 无穷小量等价代换的常用公式是什么?新闻资讯12-22
无穷小量等价代换的常用公式是什么?新闻资讯12-22 -
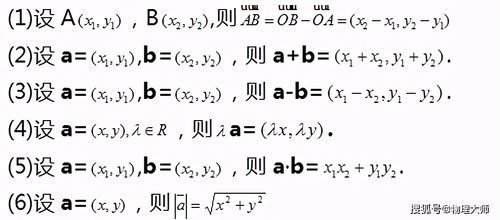 向量平行与垂直的公式是什么?新闻资讯11-05
向量平行与垂直的公式是什么?新闻资讯11-05 -
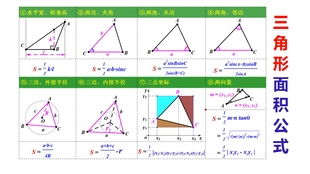 三角形面积计算公式详解新闻资讯11-25
三角形面积计算公式详解新闻资讯11-25 -
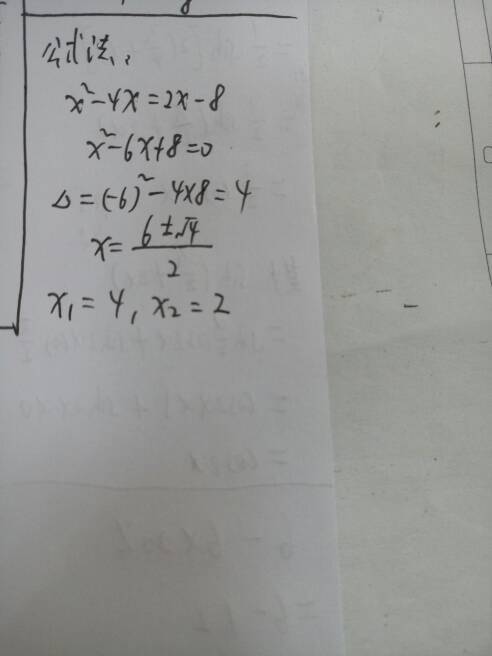 如何用公式法进行因式分解?新闻资讯11-23
如何用公式法进行因式分解?新闻资讯11-23 -
 揭秘:方差计算的神秘公式究竟是什么?新闻资讯11-09
揭秘:方差计算的神秘公式究竟是什么?新闻资讯11-09