三角形面积计算公式详解

在我们日常生活中，无论是解决数学问题还是进行简单的工程设计，了解如何计算三角形的面积都是一项基本且实用的技能。三角形作为几何学中最基本的形状之一，它的面积计算公式不仅在数学课堂上经常出现，还在许多实际场景中发挥着重要作用。那么，三角形面积公式究竟是什么？它又是如何推导出来的？本文将为您详细解答这些问题，让您对三角形面积的计算有一个全面而深入的理解。

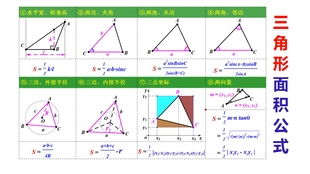
首先，我们需要明确的是，三角形面积的计算公式有多种，其中最常用也最容易理解的是海伦公式和底乘高公式。不过，对于初学者来说，底乘高公式无疑是最直观的一种。

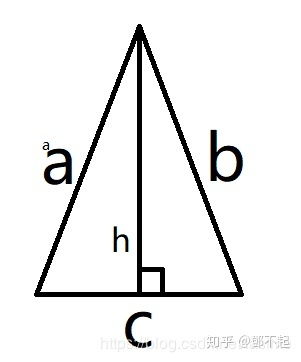
底乘高公式

底乘高公式，即面积等于底边长度乘以高再除以2，是计算三角形面积的最基本方法。这里的“底”可以是三角形的任意一条边，而“高”则是从这条边出发，垂直于这条边并到达三角形另一顶点的线段。公式表达为：

面积 = (底 × 高) ÷ 2

例如，我们有一个三角形，底边长度为8厘米，高为6厘米，那么它的面积就是：

面积 = (8厘米 × 6厘米) ÷ 2 = 24平方厘米

这个公式简单明了，易于操作，是我们在小学和初中阶段学习三角形面积计算时首先接触到的。不过，在实际应用中，有时候我们并不能直接测量到三角形的高，这时候就需要用到其他方法来计算面积了。

海伦公式

海伦公式，又称“海伦-秦九韶公式”，是一种在不知道三角形高的情况下，通过三角形的三边长度来计算面积的方法。公式表达为：

面积 = √(s(s-a)(s-b)(s-c))

其中，s是三角形的半周长，即(a+b+c)÷2，a、b、c分别是三角形的三边长度。

海伦公式的推导过程涉及到一些较为复杂的数学理论，如余弦定理和代数变换等，对于初学者来说可能较为抽象。但我们可以通过一个简单的例子来理解它的应用。

假设我们有一个三角形，三边长度分别为3厘米、4厘米和5厘米。首先，我们计算这个三角形的半周长s：

s = (3厘米 + 4厘米 + 5厘米) ÷ 2 = 6厘米

然后，我们将s和三边长度代入海伦公式中计算面积：

面积 = √(6厘米 × (6厘米 - 3厘米) × (6厘米 - 4厘米) × (6厘米 - 5厘米))

= √(6厘米 × 3厘米 × 2厘米 × 1厘米)

= 6平方厘米

通过海伦公式，我们可以在不知道三角形高的情况下，仅凭三边长度就计算出三角形的面积，这在许多实际应用中是非常方便的。

其他公式和方法

除了底乘高公式和海伦公式外，还有一些其他公式和方法可以用来计算三角形的面积，如正弦定理公式、向量法、坐标法等。这些公式和方法通常适用于特定的情况或场景，如已知三角形的顶点坐标或两角和一边等。

正弦定理公式是通过三角形的两角和一边来计算面积的，公式表达为：

面积 = (1/2)ab×sinC

其中，a和b是三角形的两边长度，C是这两边所夹的角（以弧度为单位）。这个公式在已知两角和一边的情况下非常有用。

向量法和坐标法则是通过三角形的顶点坐标来计算面积的。向量法利用了向量的叉积性质，而坐标法则通过计算顶点坐标构成的行列式来求解面积。这些方法在几何学和计算机图形学等领域有着广泛的应用。

实际应用

三角形面积的计算在日常生活和工作中有着广泛的应用。在建筑设计中，我们可能需要计算房屋或建筑的三角形区域面积来规划空间布局；在物理学中，我们可能需要计算三角形的面积来求解力或压强等问题；在计算机图形学中，我们则需要通过计算三角形的面积来实现图像的渲染和显示等。

此外，三角形面积的计算还在许多数学问题和实际应用中发挥着重要作用。例如，在求解三角形内角和、外接圆半径、内切圆半径等问题时，都需要用到三角形面积的计算公式。

总结

三角形面积公式是几何学中的重要内容之一，它不仅在数学课堂上占据重要地位，还在许多实际场景中发挥着重要作用。底乘高公式是最基本也最容易理解的方法，适用于已知底和高的情况；海伦公式则是一种在不知道三角形高的情况下，通过三边长度来计算面积的方法；正弦定理公式、向量法和坐标法则适用于特定的情况或场景。

掌握三角形面积的计算方法不仅有助于我们更好地理解和应用几何学知识，还能在实际应用中发挥重要作用。因此，我们应该认真学习并掌握这些公式和方法，以便在未来的学习和工作中能够灵活运用它们来解决实际问题。

通过以上介绍，相信您对三角形面积公式已经有了更深入的了解。无论是底乘高公式还是海伦公式等其他方法，它们都是几何学中的宝贵财富，值得我们认真学习和掌握。希望本文能够帮助您更好地理解和应用三角形面积的计算公式，为您的学习和工作带来便利。