直角三角形面积计算公式详解
直角三角形的面积计算公式,是我们在数学学习中经常会遇到的一个基础而重要的知识点。无论是在小学数学课堂上,还是在日常生活中的各种计算中,这一公式都发挥着重要的作用。今天,我们就来详细了解一下直角三角形的面积计算公式,看看它是如何推导出来的,又该如何正确应用。
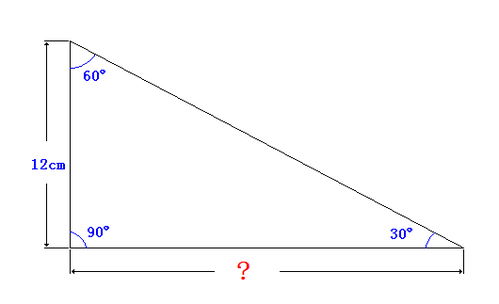
首先,我们需要明确什么是直角三角形。直角三角形是一种特殊的三角形,它有一个90度的角,我们称之为直角。在直角三角形中,除了直角外,还有两个锐角,它们的度数之和也是90度。有了这个基本概念,我们就可以进一步探讨直角三角形的面积计算公式了。
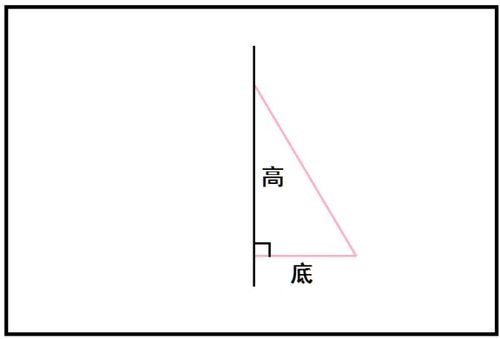
直角三角形的面积计算公式非常简洁明了:面积 = (底 × 高)÷ 2。这里的“底”和“高”是指直角三角形的两条直角边。换句话说,如果我们把一个直角三角形看作是一个由两条直角边围成的矩形的一半,那么这个矩形的面积就是底乘以高,而直角三角形的面积就是这个矩形面积的一半。
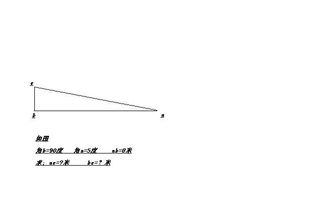
这个公式是怎么来的呢?我们可以通过一个简单的几何图形推导来理解。想象一下,我们有一个直角三角形,它的两条直角边分别是a和b,斜边是c。现在,我们做一个与这个直角三角形同底等高的矩形,那么这个矩形的面积就是a乘以b。但是,这个矩形包含了两个直角三角形,所以每个直角三角形的面积就是矩形面积的一半,即(a × b)÷ 2。
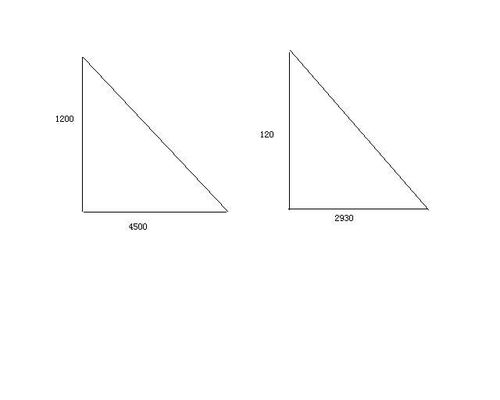
当然,这个推导过程是基于几何图形的直观理解。在更严格的数学证明中,我们可以通过平行四边形的面积公式来推导直角三角形的面积公式。具体来说,我们可以把直角三角形看作是一个平行四边形的一半。平行四边形的面积公式是底乘以高,所以直角三角形的面积就是平行四边形面积的一半,也就是(底 × 高)÷ 2。
了解了直角三角形的面积计算公式后,我们就可以在实际问题中应用这个公式了。比如,在建筑设计中,我们经常需要计算直角三角形的面积来确定材料的用量。在物理学中,直角三角形的面积也经常出现,比如在计算电场、磁场等物理量时。此外,在日常生活中,我们也可以通过测量直角三角形的两条直角边来计算它的面积,比如计算一个房间的墙面面积时,如果墙面是一个直角三角形,我们就可以用这个公式来计算。
在应用直角三角形的面积计算公式时,需要注意以下几点:
一是要确保我们计算的是直角三角形的面积。如果三角形不是直角三角形,那么这个公式就不适用。在这种情况下,我们需要使用其他方法来计算三角形的面积,比如海伦公式或者三角形的面积公式(底乘以高的一半,但这里的底和高不是直角边,而是三角形的任意一边及其对应的高)。
二是要准确测量或给出直角三角形的两条直角边的长度。在计算面积时,我们需要知道这两条边的准确长度,否则计算出来的面积就会不准确。在实际操作中,我们可以使用测量工具(如卷尺、游标卡尺等)来测量这两条边的长度。
三是要注意公式的正确应用。在计算过程中,要确保我们把正确的数值代入公式中,并且按照正确的运算顺序进行计算。如果我们把数值代入错误或者运算顺序不对,那么计算出来的面积就会是错误的。
此外,还有一些与直角三角形的面积计算公式相关的知识点值得我们注意。比如,我们可以利用这个公式来计算直角三角形的斜边长度。虽然这看起来与面积计算无关,但实际上我们可以通过面积公式和勾股定理来推导出斜边的长度。具体来说,如果我们知道直角三角形的面积和其中一条直角边的长度,就可以通过面积公式求出另一条直角边的长度,然后再利用勾股定理求出斜边的长度。
另外,我们还可以利用直角三角形的面积公式来解决一些实际问题。比如,在地理测量中,我们有时需要计算地球表面上某个直角三角形的面积。由于地球表面是一个曲面而不是平面,所以我们需要使用特殊的公式来计算这种曲面上的面积。但是,如果我们把这个曲面看作是由无数个微小的平面三角形组成的,那么我们就可以用直角三角形的面积公式来近似计算每个小三角形的面积,然后再把这些小三角形的面积加起来得到整个曲面的面积。这种方法虽然有一定的近似性,但在实际应用中通常已经足够准确了。
总之,直角三角形的面积计算公式是一个非常重要而实用的数学工具。它不仅可以帮助我们计算直角三角形的面积,还可以解决许多与直角三角形相关的实际问题。在学习和应用这个公式时,我们要注意公式的推导过程、应用条件以及注意事项等方面的问题,以确保我们能够正确地使用这个公式来解决实际问题。同时,我们也要不断探索和发现这个公式与其他数学知识点之间的联系和规律,以拓展我们的数学视野和解决问题的能力。
-
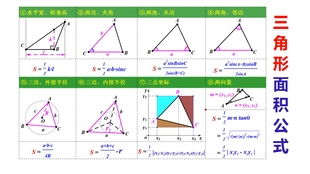 三角形面积计算公式详解新闻资讯11-25
三角形面积计算公式详解新闻资讯11-25 -
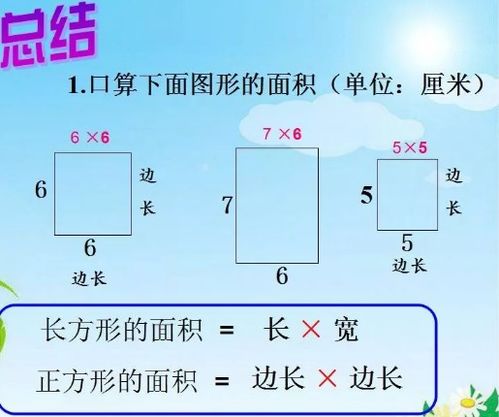 正方形面积计算公式详解新闻资讯10-25
正方形面积计算公式详解新闻资讯10-25 -
 等腰三角形面积计算方法详解新闻资讯10-31
等腰三角形面积计算方法详解新闻资讯10-31 -
 揭秘!直角三角形面积计算的神奇公式新闻资讯10-30
揭秘!直角三角形面积计算的神奇公式新闻资讯10-30 -
 等腰三角形面积公式是什么?已知腰长该如何求解?新闻资讯10-31
等腰三角形面积公式是什么?已知腰长该如何求解?新闻资讯10-31 -
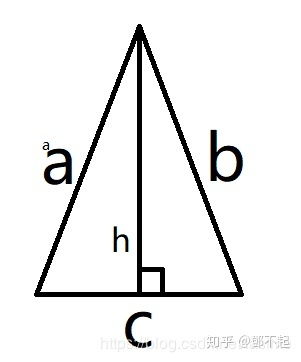 三角形面积的计算公式是什么?新闻资讯11-10
三角形面积的计算公式是什么?新闻资讯11-10











