正方形面积计算公式详解
在探讨“正方形的面积公式是什么”这一基础而重要的数学概念时,我们首先要明确正方形作为一种特殊四边形的本质特征,进而推导出其面积的计算方法。正方形,作为几何学中的基本图形之一,拥有四个等长的边和四个完全相同的直角。这一独特的性质使得正方形的面积计算变得既直观又简单。
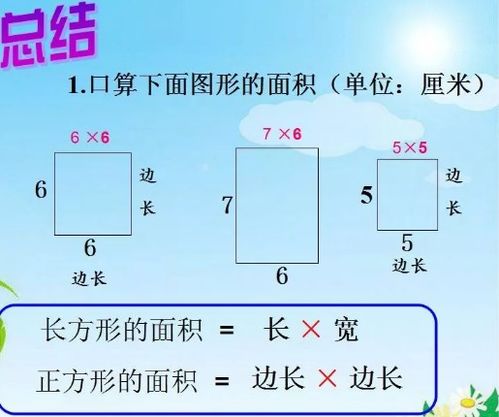
正方形的定义与特性
正方形,顾名思义,是一个所有边都相等的四边形。它具备以下几个显著特性:

1. 四边等长:正方形的四条边长度完全相等,这是定义正方形的基本条件。

2. 四个直角:正方形的四个角都是90度的直角,这一特性使其与一般的四边形区分开来。
3. 对角线相等且垂直平分:正方形的两条对角线不仅长度相等,还互相垂直且平分对方,这一性质在面积和边长的关系中起到关键作用。
4. 对称性:正方形是中心对称、轴对称的图形,这种对称性在解决相关问题时提供了便利。
正方形的面积公式推导
正方形的面积计算公式是数学中的基础知识之一,它直接来源于正方形的基本特性。要推导正方形的面积公式,我们可以从以下几个方面入手:
方法一:基于边长的直接计算
由于正方形的四边等长,我们设正方形的边长为$a$。正方形的面积可以理解为它内部包含的所有单位面积的总和。在二维平面上,如果我们选择正方形的一个边作为基准,沿着这个边并排摆放与边长相等的多个单位正方形(每个单位正方形的面积为1),直到铺满整个正方形,那么所需单位正方形的数量就等于正方形的边长$a$。接着,我们再考虑垂直于这个基准边的方向,同样地,以边长$a$为间距,摆放单位正方形直至覆盖整个正方形。显然,这个方向上也需要$a$个单位正方形。
因此,整个正方形被划分为$a \times a$个小正方形,每个小正方形的面积都是1,所以正方形的总面积就是$a \times a = a^2$。
方法二:利用对角线与面积的关系
虽然这种方法在实际计算中不如第一种直观,但它提供了另一种理解正方形面积的角度。正方形的两条对角线将正方形划分为四个全等的等腰直角三角形。如果我们能求出其中一个三角形的面积,那么正方形的面积就是其四倍。
设正方形的边长为$a$,则其对角线长度为$\sqrt{a^2 + a^2} = \sqrt{2}a$(利用勾股定理得出)。然而,直接通过对角线长度来求正方形的面积并不直接,因为这会涉及到复杂的三角函数或二次方程求解。但在理论层面,它展示了正方形面积与其几何特性(如对角线)之间的深刻联系。
正方形面积公式的应用
掌握了正方形的面积公式$S = a^2$后,我们可以轻松地解决一系列与正方形面积相关的问题。无论是计算房间地板铺设所需瓷砖的数量,还是设计花坛时估算所需草皮的面积,正方形的面积公式都是不可或缺的工具。
建筑设计:在建筑设计中,正方形房间或空间的设计常常需要考虑其面积,以确保功能性与美观性的平衡。
农业规划:在农田规划中,有时需要将土地划分为若干个正方形区域,以便进行精确的作物种植和管理,此时正方形的面积计算就显得尤为重要。
手工制作:在手工制作中,如折纸艺术、木工制作等,经常需要制作正方形的形状,了解正方形的面积有助于准确估算材料用量。
科学研究:在物理学、化学等科学研究中,正方形(或其变形如立方体)常被用作实验模型或理论模型的基础,对其面积或体积的计算是实验设计和数据分析的基础步骤之一。
结论
综上所述,“正方形的面积公式是什么”这一问题的答案简洁而明确:正方形的面积等于其边长的平方,即$S = a^2$。这一公式的推导不仅加深了我们对正方形几何特性的理解,也为我们解决实际问题提供了有力的数学工具。无论是日常生活中的小计算,还是科学研究中的复杂分析,正方形的面积公式都发挥着不可替代的作用。
-
 正方体表面积计算公式详解新闻资讯12-03
正方体表面积计算公式详解新闻资讯12-03 -
 请问正方体的表面积计算公式是怎样的?新闻资讯10-26
请问正方体的表面积计算公式是怎样的?新闻资讯10-26 -
 正方体面积的计算公式是什么?新闻资讯11-08
正方体面积的计算公式是什么?新闻资讯11-08 -
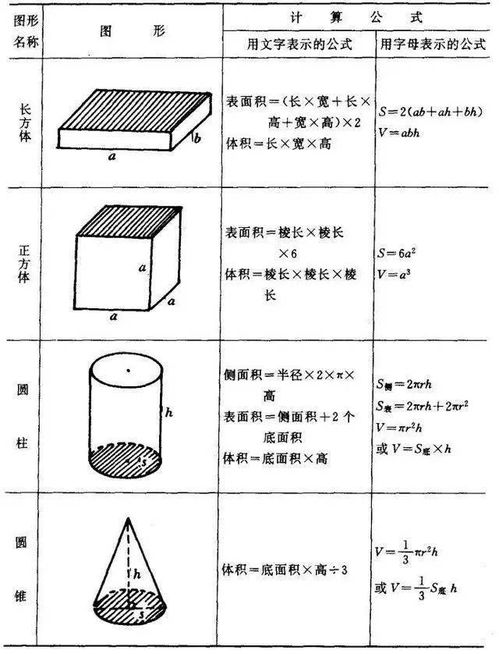 正方体的表面积计算公式是什么?新闻资讯10-20
正方体的表面积计算公式是什么?新闻资讯10-20 -
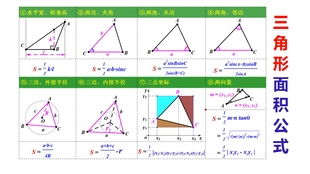 三角形面积计算公式详解新闻资讯11-25
三角形面积计算公式详解新闻资讯11-25 -
 直角三角形面积计算公式详解新闻资讯10-31
直角三角形面积计算公式详解新闻资讯10-31












