向量平行与垂直的公式是什么?
在数学领域中,向量是一个核心概念,广泛应用于物理、工程、计算机科学等多个学科。向量之间的关系,尤其是平行与垂直关系,对于理解空间结构、解决实际问题具有重要意义。向量平行与垂直的判定和计算,依赖于特定的数学公式。本文将从定义出发,逐步深入探讨向量平行与垂直的公式,并通过几何意义和坐标表示两个维度进行详细解析。
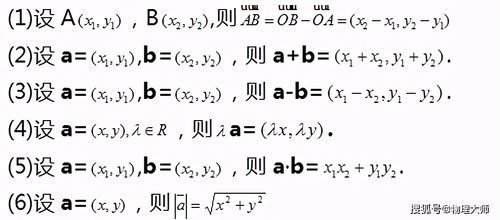
向量基础
向量是一个具有大小和方向的量,通常用带有箭头的线段表示。在数学上,向量$\vec{a}$可以由其起点$A$和终点$B$表示为$\overrightarrow{AB}$,或者简单地用有序数组$(a_1, a_2, ..., a_n)$表示,其中$n$是向量的维数。在二维平面上,向量表示为$(a, b)$;在三维空间中,向量表示为$(a, b, c)$。
向量平行的定义与公式
定义
如果两个向量$\vec{a}$和$\vec{b}$方向相同或相反,且大小可以不同,则称这两个向量平行。平行向量的一个重要性质是,一个向量可以表示为另一个向量的标量倍,即存在实数$k$,使得$\vec{a} = k\vec{b}$。
几何意义
在几何上,两个向量平行的直观表现是,它们所在的直线平行或重合。若将两向量首尾相接绘制于同一平面或空间中,可以发现它们的方向向量成比例。
坐标表示与公式
对于二维向量$\vec{a} = (a_1, a_2)$和$\vec{b} = (b_1, b_2)$,若$\vec{a}$与$\vec{b}$平行,则存在实数$k$,使得$a_1 = kb_1$且$a_2 = kb_2$。这等价于说,向量的对应分量成比例,即$\frac{a_1}{b_1} = \frac{a_2}{b_2}$(假设$b_1 \neq 0$且$b_2 \neq 0$)。特别地,当$k = -1$时,两向量方向相反。
在三维空间中,向量平行的条件类似,即$\vec{a} = (a_1, a_2, a_3)$与$\vec{b} = (b_1, b_2, b_3)$平行,当且仅当$\frac{a_1}{b_1} = \frac{a_2}{b_2} = \frac{a_3}{b_3}$(同样假设分母不为零)。
向量垂直的定义与公式
定义
如果两个向量$\vec{a}$和$\vec{b}$满足$\vec{a} \cdot \vec{b} = 0$,则称这两个向量垂直。这里的点乘(或称为内积)定义为$\vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 + ... + a_nb_n$,其中$n$是向量的维数。
几何意义
在几何上,向量垂直的直观表现是,它们所在的直线互相垂直。对于二维平面上的向量,垂直即意味着一个向量与另一个向量形成的角为$90^\circ$。在三维空间中,垂直关系同样适用于任意两个向量,即使它们不在同一平面上。
坐标表示与公式
对于二维向量$\vec{a} = (a_1, a_2)$和$\vec{b} = (b_1, b_2)$,它们垂直的条件是$\vec{a} \cdot \vec{b} = 0$,即$a_1b_1 + a_2b_2 = 0$。这一公式简洁地表达了二维向量垂直的充分必要条件。
在三维空间中,向量$\vec{a} = (a_1, a_2, a_3)$与$\vec{b} = (b_1, b_2, b_3)$垂直的条件同样为$\vec{a} \cdot \vec{b} = 0$,即$a_1b_1 + a_2b_2 + a_3b_3 = 0$。这一公式在三维空间中同样适用,是判断两个向量是否垂直的通用方法。
应用实例
平面上的向量关系
考虑二维平面上两个向量$\vec{u} = (2, 3)$和$\vec{v} = (4, 6)$。首先判断它们是否平行。计算比例$\frac{u_1}{v_1} = \frac{
- 上一篇: 2024姚基金慈善赛直播观看渠道
- 下一篇: 探索原神:揭秘蒙德地灵龛全地图分布与隐藏位置
-
 空间向量:如何判断平行与垂直?公式详解!新闻资讯11-03
空间向量:如何判断平行与垂直?公式详解!新闻资讯11-03 -
 向量平行的判定公式是什么新闻资讯11-03
向量平行的判定公式是什么新闻资讯11-03 -
 叉乘(向量积)的公式是什么?新闻资讯11-07
叉乘(向量积)的公式是什么?新闻资讯11-07 -
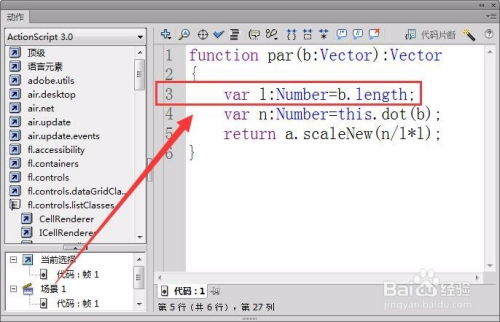 投影向量的具体计算公式详解新闻资讯10-22
投影向量的具体计算公式详解新闻资讯10-22 -
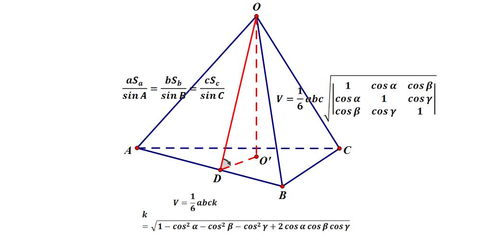 四面体体积计算公式详解新闻资讯11-09
四面体体积计算公式详解新闻资讯11-09 -
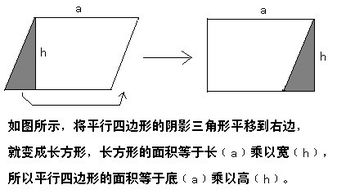 平行四边形面积计算公式详解新闻资讯11-24
平行四边形面积计算公式详解新闻资讯11-24












