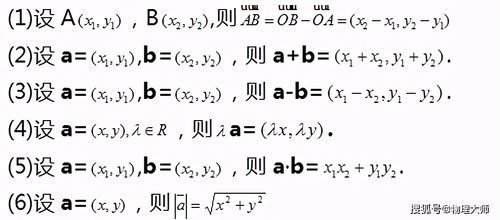投影向量的具体计算公式详解
在探讨投影向量的计算公式时,我们首先需要明确几个基本概念:向量、投影以及它们在数学和物理学中的广泛应用。向量,作为既有大小又有方向的量,是线性代数与物理学的核心概念之一。而投影向量,则是将一个向量沿着另一个向量的方向进行“压缩”或“拉长”,从而得到的与该方向平行的向量分量。这一概念在力学、光学、计算机科学等多个领域都扮演着重要角色。
投影向量的基本定义
设有两个向量a和b(其中b非零),则向量a在向量b上的投影向量记作proj_b(a)。这个投影向量proj_b(a)是a沿b方向的分量,它与b共线,且其长度(模)由a和b之间的夹角以及它们的模共同决定。

投影向量的计算公式
投影向量的计算公式直接关联到两个向量的点积(数量积)和模(长度)。具体地,向量a在向量b上的投影向量proj_b(a)可以表示为:

$$ \text{proj}_b(\textbf{a}) = \frac{\textbf{a} \cdot \textbf{b}}{\|\textbf{b}\|^2} \textbf{b} $$

其中:
a · b 表示向量a与向量b的点积,其计算公式为 a · b = |a| |b| cosθ,其中θ为两向量之间的夹角。
\|\|b\|\|^2 是向量b的模的平方,即b的长度与自身相乘。
b 是向量b本身,表示投影的方向。
分解公式理解
为了更直观地理解上述公式,我们可以将其分解为几个部分来看:
1. a · b 计算了a和b在它们共同方向上的“重叠”程度,即两向量在该方向上的分量乘积,受两向量夹角影响。
2. \|\|b\|\|^2 确保了当我们将点积除以b的模的平方时,得到的是一个标量(即没有方向的数值),这个标量代表了a在b方向上的“缩放比例”。
3. 最后,将这个缩放比例与b相乘,得到的就是a在b方向上的投影向量proj_b(a)。
应用场景示例
1. 力学中的应用
在力学中,当我们需要计算一个力在另一个力方向上的分量时,投影向量的概念就显得尤为重要。比如,一个物体受到多个力的作用,如果我们想知道其中一个力(如推力)在另一个力(如重力)方向上的影响,就可以使用投影向量的公式来计算。
2. 光学中的应用
在光学领域,特别是涉及到光的反射和折射时,光线的方向变化可以视为向量在不同介质或平面上的投影。通过计算光线的投影向量,我们可以理解光线是如何在空间中传播的,并据此设计光学系统或进行光路分析。
3. 计算机图形学
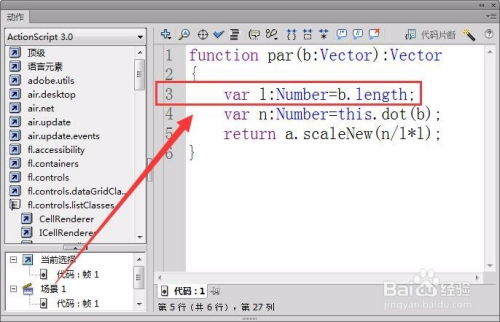
在计算机图形学中,向量投影的概念被广泛应用于3D渲染、光线追踪、碰撞检测等多个方面。例如,在渲染过程中,通过计算光线向量与物体表面法向量的投影,可以确定光线与物体的交互方式,从而生成逼真的图像效果。
结语
投影向量的计算公式是线性代数中一个重要且实用的工具,它不仅在数学理论上有着深刻的意义,还在多个学科和实际应用中发挥着不可替代的作用。掌握这一公式,不仅能帮助我们更深入地理解向量的性质和行为,还能为解决实际问题提供有力的数学支持。通过上面的介绍,相信读者已经对投影向量的计算公式有了较为全面的认识,并能在实际应用中灵活运用。
- 上一篇: 如何正确计算利息?详细步骤与方法解析
- 下一篇: 轻松掌握:计算定期存款利息的全面指南
-
 空间向量:如何判断平行与垂直?公式详解!新闻资讯11-03
空间向量:如何判断平行与垂直?公式详解!新闻资讯11-03 -
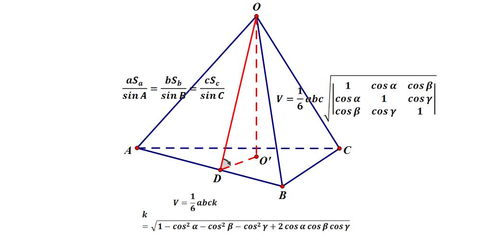 四面体体积计算公式详解新闻资讯11-09
四面体体积计算公式详解新闻资讯11-09 -
 叉乘(向量积)的公式详解新闻资讯11-14
叉乘(向量积)的公式详解新闻资讯11-14 -
 揭秘!数学中计算点到平面距离的向量公式,轻松掌握新闻资讯10-28
揭秘!数学中计算点到平面距离的向量公式,轻松掌握新闻资讯10-28 -
 向量平行与垂直的公式是什么?新闻资讯11-05
向量平行与垂直的公式是什么?新闻资讯11-05 -
 叉乘(向量积)的公式是什么?新闻资讯11-07
叉乘(向量积)的公式是什么?新闻资讯11-07