揭秘!数学中计算点到平面距离的向量公式,轻松掌握
在数学的浩瀚宇宙中,空间向量如同一把钥匙,解锁了三维世界中的无数秘密。当我们站在一个全新的维度,探索点到平面的距离这一课题时,空间向量的力量显得尤为强大而迷人。今天,就让我们一起踏上这场思维之旅,揭开“空间向量点到平面的距离公式”的神秘面纱。

探索的起点:从点到平面的距离说起
想象一下,你置身于一个广阔的三维空间中,眼前是一个平坦的平面,而你站在这个平面之外的一个点上。如何衡量你与这个平面之间的“距离”呢?这不仅仅是一个简单的测量问题,更是对空间结构和关系深刻理解的体现。在传统几何学中,我们或许会用尺子和眼睛去估算,但在数学的世界里,我们追求的是精确与普遍适用的方法——那就是利用空间向量。

空间向量的魅力
首先,让我们简单回顾一下空间向量的基本概念。向量,这个在数学和物理学中频繁出现的词汇,其实质是一种既有大小又有方向的量。在三维空间中,一个向量可以被想象成从一个点指向另一个点的有向线段。这些向量不仅帮助我们描述物体的位置和运动,还为我们提供了一种强大的工具——通过向量的运算来解析空间中的复杂关系。

点到平面距离的公式揭秘
现在,让我们正式踏入正题,探索空间向量如何帮助我们计算点到平面的距离。

假设我们有一个平面,其方程可以表示为`Ax + By + Cz + D = 0`,同时我们有一个点P,其坐标为`(x0, y0, z0)`。我们的目标是找到点P到这个平面的距离d。
公式呈现:
```
d = |Ax0 + By0 + Cz0 + D| / √(A² + B² + C²)
```
这个公式看似简单,却蕴含着深刻的数学原理。它实际上是在计算点P到平面上任意一点连线的向量(我们称之为向量a)与平面法向量(记为向量n,其方向垂直于平面,坐标为(A, B, C))之间的“垂直距离”。具体来说,就是将向量a在向量n上的投影长度作为点到平面的距离。而投影长度的计算,正是通过向量点积(数量积)与向量模长的除法来实现的。
公式背后的故事
为什么这个公式能够工作?让我们一步步来解析。
1. 法向量的作用:平面的法向量是垂直于平面的一个向量,它定义了平面的方向性。通过法向量,我们可以将三维空间中的复杂关系简化为二维或一维的运算。
2. 点积的魔力:向量a与向量n的点积(即a·n)实际上是在计算向量a在向量n方向上的投影长度乘以n的模长。但我们需要的是投影长度本身,因此还需要除以n的模长(即|n|),得到的就是a在n上的真实投影长度。
3. 绝对值的奥秘:公式中的绝对值符号是为了确保距离始终为非负值。因为向量点积的结果可能是负的,但距离作为物理量,必须是正的或零(当点在平面上时)。
实战演练:一个具体的例子
为了更直观地理解这个公式,我们来看一个具体的例子。
假设点P的坐标为(1, 2, 1),平面方程为`x + 2y + 2z - 10 = 0`。
首先,我们识别出平面方程中的A、B、C、D分别为1、2、2、-10。
然后,将点P的坐标代入公式:`d = |1*1 + 2*2 + 2*1 - 10| / √(1² + 2² + 2²)`。
计算得到:`d = |-3| / √(1+4+4) = 3 / 3 = 1`。
所以,点P到平面的距离是1个单位长度。
结语
通过空间向量,我们不仅计算出了点到平面的距离,更深刻理解了三维空间中的几何关系。这个公式的推导和应用,不仅是数学技巧的展现,更是对空间想象能力和逻辑推理能力的锻炼。在未来的学习和探索中,空间向量将继续成为我们探索未知世界的得力助手,引领我们走进更加精彩的数学世界。
希望这次旅程能让你对“空间向量点到平面的距离公式”有了更深的理解和兴趣。数学之美,在于它无尽的奥秘和广泛的应用,让我们继续在这条充满挑战与发现的道路上前行吧!
- 上一篇: A4纸张的尺寸是几次方几的倍数?
- 下一篇: 一键清空!轻松删除抖音观看历史视频的步骤
-
 揭秘!如何轻松计算点到平面的距离?超实用距离公式大公开!新闻资讯10-28
揭秘!如何轻松计算点到平面的距离?超实用距离公式大公开!新闻资讯10-28 -
 揭秘!直角坐标系中两点距离计算的神秘公式,你知道吗?新闻资讯10-23
揭秘!直角坐标系中两点距离计算的神秘公式,你知道吗?新闻资讯10-23 -
 揭秘!椭圆面积公式的计算方法,轻松掌握新闻资讯10-21
揭秘!椭圆面积公式的计算方法,轻松掌握新闻资讯10-21 -
 揭秘!轻松掌握圆的周长计算方法,让数学不再绕圈圈新闻资讯10-28
揭秘!轻松掌握圆的周长计算方法,让数学不再绕圈圈新闻资讯10-28 -
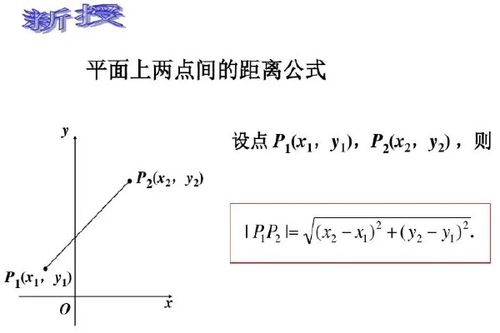 揭秘!两点间距离公式的神奇奥秘,让距离计算变得如此简单新闻资讯10-23
揭秘!两点间距离公式的神奇奥秘,让距离计算变得如此简单新闻资讯10-23 -
 叉乘(向量积)的公式是什么?新闻资讯11-07
叉乘(向量积)的公式是什么?新闻资讯11-07