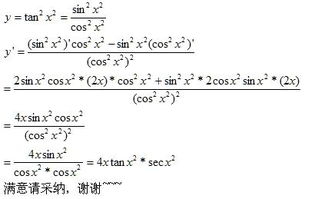arctanx(反正切函数)的表达式或等价公式是什么?
在数学的浩瀚宇宙中,隐藏着无数奇妙的秘密与公式,它们如同星辰般璀璨,引领着探索者一步步深入未知的领域。今天,就让我们一起揭开一个既古老又常新的数学之谜——`arctanx`,这个名字听起来或许有些抽象,但它背后所蕴含的数学魅力与实际应用,定能让你眼前一亮,感受到数学的无穷魅力。

探寻`arctanx`的秘密花园
想象一下,你正漫步在一片神秘的数学花园里,四周被各种奇妙的函数图像环绕。突然,你发现了一片被柔和光线笼罩的区域,那里盛开着一朵名为“反正切函数”的花朵,它的名字就叫`arctanx`。这朵花不仅外表迷人,更隐藏着通往另一个数学世界的秘密通道。
从三角函数到`arctanx`的蜕变
要理解`arctanx`,我们不得不先从它的“前身”——三角函数说起。在三角学的广阔天地里,正弦(sin)、余弦(cos)和正切(tan)是三位耀眼的明星。特别是正切函数,它描述了在直角三角形中,对边长度与邻边长度之比的关系。而`arctanx`,全称“反正切函数”,则是正切函数的“逆操作”。
简单来说,如果你知道一个角的正切值`x`,想要知道这个角具体是多少度或多少弧度,`arctanx`就能帮你找到答案。它就像是一个解密器,能够将正切值转换回对应的角度。
`arctanx`的数学表达式与性质
数学上,`arctanx`没有直接的“等于什么”的公式,因为它本身就是一个定义良好的函数,用于表示所有满足`tan(θ) = x`的`θ`值,其中`θ`的范围被限制在`(-π/2, π/2)`内,这是为了保证函数的单值性和连续性。不过,我们可以通过一些性质来更深入地了解它:
1. 奇函数性质:`arctan(-x) = -arctan(x)`,这意味着反正切函数是关于原点对称的。
2. 增减性:在定义域内,`arctanx`是单调递增的,即随着`x`的增大,`arctanx`的值也在增大。
3. 极限性质:当`x`趋近于正无穷时,`arctanx`趋近于`π/2`;当`x`趋近于负无穷时,`arctanx`趋近于`-π/2`。
`arctanx`的实用场景
`arctanx`不仅停留在理论层面,它在多个领域都有着广泛的应用。
工程与物理学
在工程领域,尤其是在信号处理、控制系统设计等方面,`arctanx`常被用于计算相位角,这对于理解和控制系统的动态行为至关重要。在物理学中,它可用于求解物体在特定角度下的运动状态,比如弹道计算中的倾斜角度。
经济学与金融学
在经济学和金融学领域,`arctanx`可能不那么直接出现,但它背后的概念——即反函数的概念,对于理解经济模型的复杂关系、预测市场趋势等具有重要作用。例如,在回归分析中,通过求解参数的反正切值,可以分析变量之间的相关性及其影响方向。
计算机科学
在计算机图形学、游戏开发等领域,`arctanx`(及其变体,如`atan2`)被用于计算物体间的相对方向、角度,实现真实的视觉效果和物理交互。它是实现3D图形渲染、碰撞检测等功能的基石之一。
走进`arctanx`的心灵深处
每当我们提起`arctanx`,实际上是在与数学历史长河中无数先辈的智慧对话。它不仅仅是一个公式,更是人类探索未知、追求真理的见证。通过`arctanx`,我们学会了如何用数学的语言去描述和预测现实世界中的现象,感受到了数学与生活的紧密联系。
结语
在这个简短的探索之旅中,我们一同揭开了`arctanx`的神秘面纱,领略了它的数学魅力和广泛应用。正如数学本身一样,`arctanx`既是简洁的,又是深邃的,它引领我们穿梭于理论与实践之间,享受着思考的乐趣和发现的惊喜。下次当你在数学或生活的某个角落再次遇见`arctanx`时,不妨停下来,细细品味它背后的故事与意义,相信你会有不一样的收获和感悟。
-
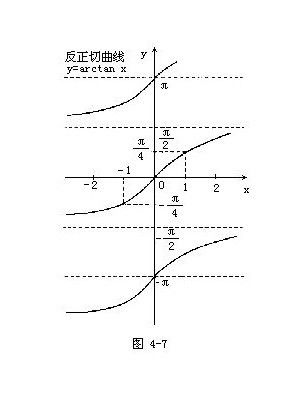 如何绘制和理解反正切函数(Arctan)的图像及其特征?新闻资讯10-23
如何绘制和理解反正切函数(Arctan)的图像及其特征?新闻资讯10-23 -
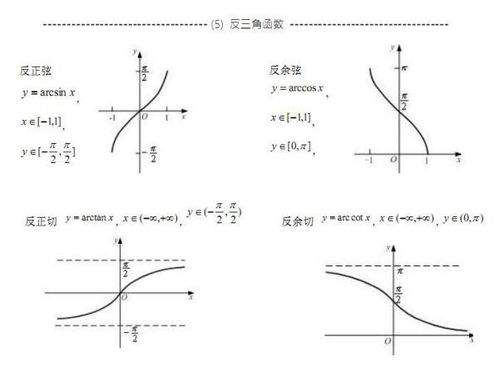 arc三角函数的导数分别是什么?新闻资讯11-22
arc三角函数的导数分别是什么?新闻资讯11-22 -
 无穷小量等价代换的常用公式是什么?新闻资讯12-22
无穷小量等价代换的常用公式是什么?新闻资讯12-22 -
 Q&A: 轻松掌握!如何用计算器计算反三角函数arctan?新闻资讯11-02
Q&A: 轻松掌握!如何用计算器计算反三角函数arctan?新闻资讯11-02 -
 等价无穷小公式是什么?初学者如何理解和应用这些公式?新闻资讯12-22
等价无穷小公式是什么?初学者如何理解和应用这些公式?新闻资讯12-22 -
 tan x 的导数是多少?如何求导?新闻资讯12-22
tan x 的导数是多少?如何求导?新闻资讯12-22