tan x 的导数是多少?如何求导?
在探索数学的浩瀚宇宙中,导数作为微积分的核心概念之一,扮演着连接静态数学与动态世界变化的桥梁角色。当我们聚焦于“tan x的导数等于什么”这一具体问题时,实际上是在揭开三角函数导数特性的神秘面纱,特别是正切函数(tan x)随其角度(或更准确地说是弧度)变化时,其斜率(即导数)的变化规律。
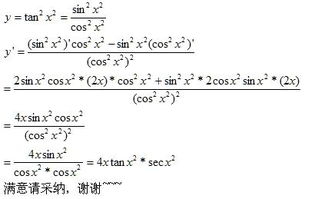
正切函数的基础回顾
首先,让我们简要回顾一下正切函数(tan x)的定义。在直角坐标系中,给定一个角x(其大小以弧度为单位),该角对应的正切值定义为对边长度除以邻边长度,在单位圆(半径为1的圆)上,这等价于从原点出发、与x轴正方向成x弧度的射线与单位圆交点的y坐标除以x坐标。因此,tan x在很多数学、物理及工程问题中都是非常重要的工具,尤其是在处理角度与边长关系的问题时。
导数的意义
导数,简而言之,是描述函数在某一点附近变化率的数学工具。对于任意函数f(x),其在x点的导数f'(x)表示函数在该点附近的微小变化量与自变量微小变化量之比的极限值。在几何上,这可以理解为函数图像在该点处切线的斜率。导数的计算和应用不仅限于几何解释,它还广泛涉及物理学中的速度、加速度分析,经济学中的边际成本、边际收益等问题。
tan x的导数推导
现在,我们直接进入主题——“tan x的导数等于什么”。为了找到tan x的导数,我们可以利用三角恒等式和基本导数规则来推导。
正切函数可以表示为两个基本三角函数(正弦和余弦)的比值,即tan x = sin x / cos x。要求tan x的导数,我们可以使用商的导数公式,该公式表述为:(u/v)' = (u'v - uv') / v²,其中u和v分别是被除数和除数,u'和v'分别是它们的导数。
将sin x视为u,cos x视为v,则u' = cos x(正弦函数的导数),v' = -sin x(余弦函数的导数,注意负号)。代入商的导数公式,我们得到:
(tan x)' = [(cos x * 0 - sin x * (-sin x)) / cos² x]
= (sin² x) / cos² x
由于cos² x + sin² x = 1(三角恒等式),我们可以将上式进一步化简为:
(tan x)' = (sin² x) / (1 - sin² x)
但更常见的形式是利用sec² x(即1/cos² x)来表示,因为:
(tan x)' = sin x * (1/cos x) * (-sin x / cos x) 的负号被上面的正号抵消,得
(tan x)' = (sin x / cos x) * (sin x / cos x)
= (sin² x) / (cos² x)
= 1 / (1 / sin² x)
= 1 / cos² x
= sec² x
因此,tan x的导数最终可以简洁地表示为sec² x。
导数的几何与物理意义
几何上,tan x的导数sec² x表示tan x函数图像在某点处切线的斜率。由于sec² x总是非负的(因为余弦值的平方不可能为负),且当x接近π/2 + kπ(k为整数)时,sec² x趋于无穷大,这反映了tan x在这些点附近的陡峭变化,即正切函数在这些点上不连续。
在物理应用中,tan x的导数可能与某些依赖于角度变化的物理量的变化率有关,尽管直接的例子可能不如速度、加速度等直观,但它仍然是理解和分析复杂物理现象时不可或缺的数学工具。
结语
通过上述分析,我们不仅解答了“tan x的导数等于什么”的问题,还深入探讨了导数的概念、三角函数的导数推导过程,以及这些知识在几何和物理中的潜在应用。数学之美,在于其逻辑的严谨性和应用的广泛性,而导数作为连接数学理论与现实世界的纽带,更是展现了这种美的精髓。希望这篇文章能够激发你对数学更深层次的兴趣和探索欲望。
-
 分数求导的奥秘与技巧新闻资讯11-05
分数求导的奥秘与技巧新闻资讯11-05 -
 深入解析:指数函数求导的定义与AMP技巧巧妙推导新闻资讯10-28
深入解析:指数函数求导的定义与AMP技巧巧妙推导新闻资讯10-28 -
 分数的导数求解方法新闻资讯11-05
分数的导数求解方法新闻资讯11-05 -
 轻松掌握:log函数求导公式详解新闻资讯11-09
轻松掌握:log函数求导公式详解新闻资讯11-09 -
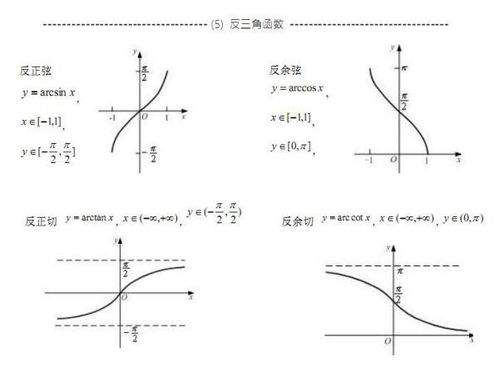 arc三角函数的导数分别是什么?新闻资讯11-22
arc三角函数的导数分别是什么?新闻资讯11-22 -
 揭秘!secx的导数究竟是什么?新闻资讯10-27
揭秘!secx的导数究竟是什么?新闻资讯10-27