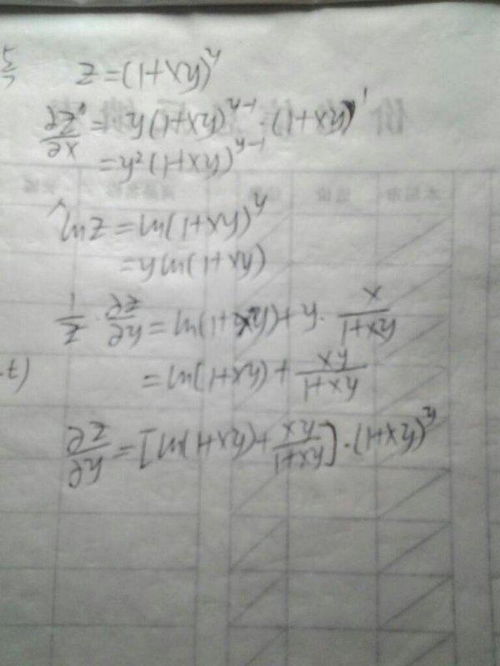揭秘!secx的导数究竟是什么?
当我们探讨数学中三角函数的导数时,特别是针对正割函数(secant function),记作secx的导数,这是一个既基础又关键的知识点,它在微积分学、物理学、工程学等多个领域都有广泛应用。下面,我们就直接而清晰地来解答这个问题:secx的导数是什么。
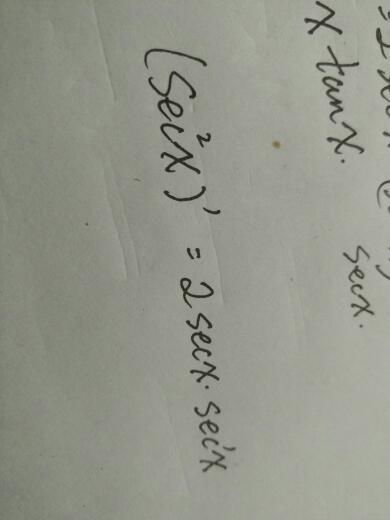
secx的导数解析
首先,我们需要明确secx的定义。在三角函数中,secx定义为余弦函数cosx的倒数,即:

\[ \sec x = \frac{1}{\cos x} \]
要求解secx的导数,我们可以利用商的导数公式(即(u/v)' = (u'v - uv')/v²),其中u=1(常数的导数为0),v=cosx。将这两个函数代入商的导数公式中,我们得到:
\[ (\sec x)' = \left( \frac{1}{\cos x} \right)' = \frac{0 \cdot \cos x - 1 \cdot (-\sin x)}{\cos^2 x} \]
这里,cosx的导数是-sinx(由三角函数导数的基本公式给出)。
进一步化简上述表达式,得到:
\[ (\sec x)' = \frac{\sin x}{\cos^2 x} \]
但是,我们注意到分子分母都含有cosx的项,且分母是cosx的平方,这提示我们可以利用三角函数的一个基本恒等式进行进一步化简:
\[ \tan x = \frac{\sin x}{\cos x} \]
将tanx的表达式代入之前得到的导数公式中,我们得到:
\[ (\sec x)' = \frac{\sin x}{\cos^2 x} = \frac{1}{\cos x} \cdot \frac{\sin x}{\cos x} = \sec x \cdot \tan x \]
因此,secx的导数最终可以表示为:
\[ (\sec x)' = \sec x \cdot \tan x \]
理解与应用
了解secx的导数不仅有助于我们深化对三角函数导数的理解,还在许多实际问题中发挥着重要作用。例如,在物理学中,当处理涉及力、加速度和位移的问题时,经常需要用到三角函数及其导数来描述周期性变化或振动现象。
此外,在工程学领域,如电路分析、信号处理等方面,secx及其导数也扮演着重要角色。例如,在解决涉及交流电路的问题时,电压和电流可能会以正弦或余弦波形式变化,此时就需要用到三角函数的导数来求解相关的微分方程。
结论
综上所述,secx的导数是secx乘以tanx,即(\(\sec x\))' = \(\sec x \cdot \tan x\)。这一结论不仅是三角函数导数学习中的一个重要知识点,也是连接数学与众多实际应用领域的桥梁。通过深入理解并熟练掌握这一导数公式,我们可以更好地应用数学知识解决实际问题,提升我们的科学素养和解决问题的能力。
-
 你知道secx的导数究竟是什么吗?新闻资讯10-31
你知道secx的导数究竟是什么吗?新闻资讯10-31 -
 如何求解偏导数?新闻资讯11-23
如何求解偏导数?新闻资讯11-23 -
 揭秘:secx 的真正含义是什么?新闻资讯11-10
揭秘:secx 的真正含义是什么?新闻资讯11-10 -
 求解secx积分的三种常见方法是什么?新闻资讯10-27
求解secx积分的三种常见方法是什么?新闻资讯10-27 -
 揭秘显卡:它究竟是什么?又有何神奇功能?新闻资讯11-06
揭秘显卡:它究竟是什么?又有何神奇功能?新闻资讯11-06 -
 揭秘!神仙肉究竟是什么肉?家常做法大公开!新闻资讯11-23
揭秘!神仙肉究竟是什么肉?家常做法大公开!新闻资讯11-23