你知道secx的导数究竟是什么吗?
secx的导数探秘

在数学的广阔天地中,三角函数占据着举足轻重的地位,它们不仅在几何学、物理学和工程学等多个领域有着广泛的应用,而且在微积分学中也扮演着至关重要的角色。secx函数,作为三角函数家族的一员,其导数问题不仅是理论研究的热点,也在实际应用中发挥着不可替代的作用。本文将深入探讨secx函数的导数,从定义、求解过程到应用实例,力求为读者呈现一个全面而系统的知识框架。

一、secx函数的定义与性质
secx函数,全称正割函数,是直角三角形斜边与某个锐角的邻边的比值,在数值上等于余弦函数的倒数,即secx = 1/cosx。这一定义揭示了secx与cosx之间的紧密联系,也为我们后续求解secx的导数提供了重要的线索。

secx函数具有一些独特的性质,其中最为显著的是其偶函数特性,即sec(-x) = secx。这一性质使得secx的图像关于y轴对称,为我们理解和分析secx函数的性质提供了便利。

二、secx导数的求解过程
在微积分中,导数描述了函数值对自变量的变化率,是分析函数性质的重要工具。对于secx函数而言,其导数的求解过程需要运用到复合函数求导法则和三角函数的导数公式。
具体来说,secx的导数可以通过以下步骤求解:
1. 确定secx的表达式:secx = 1/cosx。
2. 应用复合函数求导法则:将secx视为u = cosx的复合函数f(u) = 1/u,然后分别对u和f(u)求导。
3. 利用三角函数的导数公式:已知(cosx)' = -sinx,代入复合函数求导法则中。
4. 进行代数化简:结合上述步骤,得到secx的导数为(secx)' = (1/cosx)' = (-sinx)/(cos²x)。
5. 利用三角恒等式化简:注意到(-sinx)/(cos²x)可以化简为secx * tanx,因为tanx = sinx/cosx。
综上所述,secx的导数为secx * tanx。这一结果不仅揭示了secx函数与tanx函数之间的内在联系,也为我们后续分析secx函数的性质提供了重要的数学工具。
三、secx导数的几何意义与物理应用
secx的导数不仅在数学上具有理论价值,而且在几何学和物理学等实际应用领域中也发挥着重要作用。
几何意义
从几何的角度来看,secx的导数反映了函数曲线的斜率变化情况。当x的值发生变化时,secx函数值也会相应发生变化。导数就是描述这种变化的速率,即函数值对自变量的变化率。对于secx函数而言,其导数d(secx)/dx表示了切线与x轴的夹角的变化率。这一变化率反映了函数曲线在该点的凹凸性质,为我们分析函数的性质提供了重要依据。
物理应用
在物理学中,secx函数常用于描述斜面上物体的运动。由于斜面的倾角与secx函数密切相关,因此secx的导数能够反映物体加速度的变化情况。这一特性使得secx的导数在动力学分析、振动分析等领域中具有广泛的应用价值。
此外,在工程领域,secx函数也广泛应用于电路分析、天线设计等问题中。secx的导数在求解电路中的电流、电压等物理量时发挥着重要作用。通过对secx导数的深入理解,工程师们可以更好地设计和优化电路系统,提高系统的性能和稳定性。
四、secx导数在实际问题中的应用实例
为了更好地理解secx导数的应用,以下给出几个实际问题中的应用实例:
实例一:电路分析中的应用
在电路分析中,经常需要求解电流、电压等物理量随时间的变化情况。假设有一个由电阻、电感和电容组成的电路系统,其中某个元件的电压与secx函数相关。为了求解该元件的电流变化情况,我们需要利用secx的导数来求解电压对时间的导数,即电压的变化率。通过这一过程,我们可以得到电流随时间的变化情况,为电路系统的设计和优化提供重要的参考依据。
实例二:振动分析中的应用
在振动分析中,secx函数的周期性和导数的变化率可以帮助我们研究周期性振动的性质和行为。例如,在机械振动系统中,某个质点的位移与secx函数相关。为了分析该质点的振动特性,我们需要利用secx的导数来求解位移对时间的导数,即速度的变化情况。通过这一过程,我们可以得到质点的速度、加速度等物理量随时间的变化情况,为振动系统的设计和优化提供重要的参考依据。
实例三:信号处理中的应用
在信号处理领域,secx函数及其导数也发挥着重要作用。例如,在数字信号处理中,经常需要对信号进行滤波、去
- 上一篇: 揭秘!湘赣皖苏沪:它们分别代表哪些省份与城市?
- 下一篇: 揭秘:蜜罐技术全解析
-
 揭秘!secx的导数究竟是什么?新闻资讯10-27
揭秘!secx的导数究竟是什么?新闻资讯10-27 -
 揭秘!你知道古兵器‘槊’究竟是什么吗?新闻资讯11-01
揭秘!你知道古兵器‘槊’究竟是什么吗?新闻资讯11-01 -
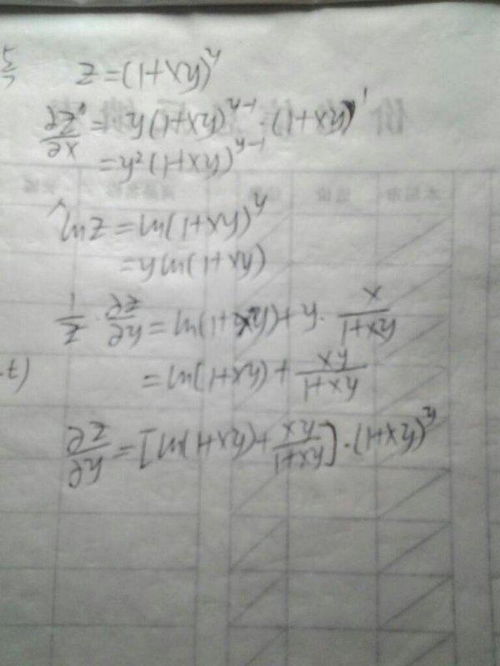 如何求解偏导数?新闻资讯11-23
如何求解偏导数?新闻资讯11-23 -
 揭秘!你知道五更究竟是几点钟吗?新闻资讯10-26
揭秘!你知道五更究竟是几点钟吗?新闻资讯10-26 -
 揭秘!你知道一英尺究竟是多长吗?新闻资讯10-25
揭秘!你知道一英尺究竟是多长吗?新闻资讯10-25 -
 《你知道吗?《西厢记》的作者究竟是谁?》新闻资讯11-02
《你知道吗?《西厢记》的作者究竟是谁?》新闻资讯11-02