正弦定理与余弦定理的定义及解析
在数学的浩瀚宇宙中,正弦定理与余弦定理如同璀璨的双星,不仅照亮了平面几何的夜空,更为解决三角形相关问题提供了强有力的工具。它们不仅仅是数学公式,更是连接几何直观与代数运算的桥梁,深刻体现了数学内部的和谐与统一。本文将从历史渊源、定义解析、应用场景、几何直观、代数证明及教育意义等多个维度,探索正弦定理与余弦定理的魅力所在。
历史渊源:数学智慧的结晶
追溯至古希腊时期,数学家们就开始了对三角形的深入研究,为后来的正弦定理和余弦定理奠定了基础。正弦定理的雏形可见于欧几里得《几何原本》中关于三角形的论述,而正式的形式化表达则要到16世纪,由荷兰数学家雷蒙多·洛必达(或译为罗伯瓦)在其著作中明确提出。余弦定理的出现稍晚一些,其完整形式由法国数学家弗朗索瓦·韦达在16世纪末期给出。这两位数学家的贡献,使得这两个定理得以系统化、理论化,成为数学史上的重要里程碑。
定义解析:几何与代数的完美融合
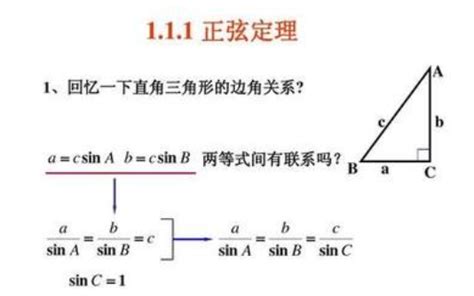
正弦定理(Sine Theorem)表述为:在任何三角形ABC中,边长a、b、c与对应角A、B、C的正弦值之比相等,即:
\[ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R \]
其中,R为三角形外接圆的半径。正弦定理揭示了三角形边长与其对应角正弦值之间的比例关系,是连接三角形的边与角的一座桥梁。
余弦定理(Cosine Theorem)则描述了三角形任意一边的平方等于其他两边的平方和减去这两边与其夹角的余弦的积的两倍,即:
\[ c^2 = a^2 + b^2 - 2ab\cos C \]
(以及对应的A、B角的公式)。余弦定理直接关联了三角形的三边长度与它们之间的夹角,是求解三角形边长的有力工具。
应用场景:解决实际问题的利器
正弦定理与余弦定理在解决三角形相关问题上展现出了强大的实用性。例如,在航海、测绘、建筑等领域,常常需要利用这些定理来计算距离、角度或高度。在航空航天领域,它们也被用于卫星定位、轨道计算等复杂问题中。此外,在物理学的波动现象、信号处理等分支,正弦与余弦函数作为基础,其定理的应用同样广泛。
在日常生活和学习中,正弦定理和余弦定理也频繁出现。比如,在解决三角形面积问题时,结合正弦定理可以快速求得;而在处理涉及角度变化的力学问题时,余弦定理则能帮助我们理解力、位移与角度之间的关系。
几何直观:图形背后的数学逻辑
正弦定理的几何直观体现在外接圆上。想象一个三角形ABC及其外接圆,从圆心O向三角形的三个顶点A、B、C作射线,分别交圆于点A'、B'、C'(其中A'与A重合,同理B'与B、C'与C),则OA = OB = OC = R(外接圆半径)。根据圆的性质,角AOB'、BOC'、COA'分别是角A、B、C的补角的一半,即半角。因此,\(\sin A = \frac{a}{2R}\)(利用正弦定义在直角三角形中的应用),同理可得其他两边的正弦关系,从而验证了正弦定理。
余弦定理的几何直观则体现在将三角形视为一个向量空间中的图形。若将三角形ABC的边AB、BC视为向量,则AC = AB - BC(向量减法)。根据向量数量积的定义,\(AC \cdot AC = (AB - BC) \cdot (AB - BC) = AB \cdot AB + BC \cdot BC - 2AB \cdot BC\cos C\),化简后即得余弦定理。这一推导过程不仅展示了余弦定理的来源,也体现了向量方法在处理几何问题中的强大功能。
代数证明:严谨的逻辑推理
正弦定理的代数证明通常依赖于三角形内角和定理、正弦函数的性质以及外接圆的性质。证明过程可能涉及构造辅助线、利用相似三角形等技巧,最终推导出边长与正弦值之间的比例关系。
余弦定理的代数证明则更为直观,可通过向量方法、坐标几何或利用余弦函数的定义来证明。向量方法如上所述,坐标几何方法则是通过设定三角形顶点的坐标,利用距离公式和夹角公式直接推导出余弦定理。而利用余弦函数的定义证明,则需在三角形内作高,通过直角三角形中的余弦关系逐步推导。
教育意义:培养逻辑思维与创新能力
正弦定理与余弦定理的学习,不仅仅是掌握几个公式的过程,更是培养逻辑思维能力、空间想象能力和数学创新能力的重要途径。通过定理的推导与应用,学生可以深刻理解数学中的抽象与具体、一般与特殊之间的关系,学会用数学的眼光观察世界,用数学的语言描述现象,用数学的方法解决问题。
此外,正弦定理与余弦定理的学习还能够激发学生对数学的兴趣,引导他们探索数学之美。这两个定理不仅在数学内部有着广泛的应用,也是连接数学与其他学科,如物理、工程、计算机科学的桥梁。通过解决实际问题,学生能够感受到数学的实用价值和魅力,从而更加热爱数学,愿意投身于数学的学习和研究中。
总之,正弦定理与余弦定理不仅是数学宝库中的瑰宝,更是人类智慧的结晶。它们以简洁的形式、深刻的内涵,展现了数学的力量与美。在学习和探索的过程中,让我们一同领略这两个定理的风采,感受数学世界的无限可能。
- 上一篇: 探索祖玛阁:揭秘神秘通行之路
- 下一篇: 新人必看:VLOOKUP技巧大揭秘,轻松实现两表数据精准匹配
-
 正弦定理和余弦定理分别是什么?新闻资讯11-09
正弦定理和余弦定理分别是什么?新闻资讯11-09 -
 揭秘!韦达定理公式全解析:你不得不知的数学奥秘新闻资讯10-20
揭秘!韦达定理公式全解析:你不得不知的数学奥秘新闻资讯10-20 -
 初中三角形知识大全:定理、公理与定义详解新闻资讯11-03
初中三角形知识大全:定理、公理与定义详解新闻资讯11-03 -
 切割线定理的详细证明过程新闻资讯11-23
切割线定理的详细证明过程新闻资讯11-23 -
 中位线定理的证明方法新闻资讯11-26
中位线定理的证明方法新闻资讯11-26 -
 揭秘:积分中值定理的核心公式大公开!新闻资讯10-25
揭秘:积分中值定理的核心公式大公开!新闻资讯10-25











