中位线定理的证明方法
在数学的浩瀚宇宙中,中位线定理犹如一颗璀璨的星辰,它以其独特的魅力和广泛的应用性,在几何学中占据着举足轻重的地位。这个定理不仅简洁明了,而且极具实用性,能够帮助我们解决许多看似复杂的问题。那么,你是否曾经好奇过,中位线定理究竟是如何被证明的?今天,就让我们一同揭开它的神秘面纱,探索这一几何瑰宝背后的逻辑之美。
首先,我们需要明确中位线的定义。在一个三角形中,连接两个中点(即两个边的中点)的线段,被称为这个三角形的中位线。而中位线定理则断言:三角形的中位线平行于第三边,并且等于第三边长度的一半。这个定理看似简单,却蕴含着丰富的几何知识和深刻的数学原理。

为了证明中位线定理,我们可以采用多种方法。其中,构造辅助线的方法最为直观且易于理解。不妨以三角形ABC为例,D、E分别是AB、AC的中点,DE为三角形ABC的中位线。我们的目标是证明DE平行于BC,且DE=1/2BC。

第一步:构造辅助线
首先,我们可以在三角形ABC外构造一个与三角形ABC相似且边长为两倍的三角形A'B'C'。具体做法是,延长BC至点C',使得BC'=CC',然后分别连接AC'、AB'(其中B'在AC'的延长线上,且AB'=AC'),得到三角形A'B'C'。接下来,我们连接A'D、A'E,并取A'B'的中点为D',A'C'的中点为E'。
第二步:利用平行四边形的性质
由于四边形B'ECC'和四边形B'DAA'都是平行四边形(对角线互相平分),根据平行四边形的性质,我们有B'E平行于CC',B'D平行于AA'。又因为D、E分别是AB、AC的中点,D'、E'分别是A'B'、A'C'的中点,所以DE平行于B'E,且DE=1/2B'E。同理,DE也平行于B'D,且DE=1/2B'D。
第三步:证明中位线与第三边平行
由于B'E平行于CC',且CC'与BC在同一直线上,所以B'E也平行于BC。又因为DE平行于B'E,所以DE也平行于BC。这就证明了中位线DE平行于三角形的第三边BC。
第四步:证明中位线长度等于第三边长度的一半
接下来,我们需要证明DE=1/2BC。由于B'D平行于AA',且AA'与BC不在同一直线上,我们可以过点D作DF平行于BC交AC于点F。由于DF平行于BC,根据平行线的性质,我们有∠ADF=∠ABC(内错角相等)。又因为∠A=∠A(公共角),且AD=AB'/2=AC/2(因为D是AB的中点,A'D是A'B'的一半,而A'B'=2AB),所以根据三角形的相似性质,我们得到三角形ADF与三角形ABC相似,且相似比为1:2。因此,DF=1/2BC。
又因为四边形DFEC是平行四边形(对角线DE、FC互相平分,由于E是AC的中点,所以F也是DC的中点),所以DE=FC=DF=1/2BC。这就证明了中位线DE的长度等于第三边BC长度的一半。
第五步:总结与反思
通过上述步骤,我们成功地证明了三角形的中位线定理。这个证明过程不仅展示了数学推理的严谨性,也体现了数学方法的灵活性。通过构造辅助线、利用平行四边形的性质、相似三角形的性质等几何知识,我们逐步推导出了中位线的性质。
然而,值得注意的是,虽然上述证明过程采用了构造辅助线的方法,但并不意味着这是唯一的方法。在数学中,往往存在着多种不同的证明方法。每一种方法都有其独特的魅力和价值,它们或简洁明了,或富有启发性,或能够帮助我们更好地理解数学概念和原理。
此外,中位线定理的应用也极为广泛。它不仅在几何学中发挥着重要作用,还在物理学、工程学等领域中有着重要的应用价值。例如,在建筑设计、机械设计等领域中,我们经常需要利用中位线定理来计算和确定某些尺寸和位置关系。因此,掌握和理解中位线定理的证明方法和应用技巧对于我们来说具有非常重要的意义。
综上所述,中位线定理是几何学中的一个重要定理。它以其简洁明了的表述和广泛的应用性而备受瞩目。通过构造辅助线、利用几何性质等方法,我们可以成功地证明这个定理。同时,掌握和理解这个定理的证明方法和应用技巧也能够帮助我们更好地解决数学问题并应用于实际生活中。因此,让我们一同珍视这颗数学宇宙中的璀璨星辰——中位线定理吧!
- 上一篇: 夜半时分,钟声悠悠传客船
- 下一篇: 脚盆鸡梗的由来解析
-
 问答揭秘:如何轻松验证直角三角形斜边中线的独特定理?新闻资讯10-26
问答揭秘:如何轻松验证直角三角形斜边中线的独特定理?新闻资讯10-26 -
 切割线定理的详细证明过程新闻资讯11-23
切割线定理的详细证明过程新闻资讯11-23 -
 揭秘平行线的魔力:线段比例分割的奥秘新闻资讯11-11
揭秘平行线的魔力:线段比例分割的奥秘新闻资讯11-11 -
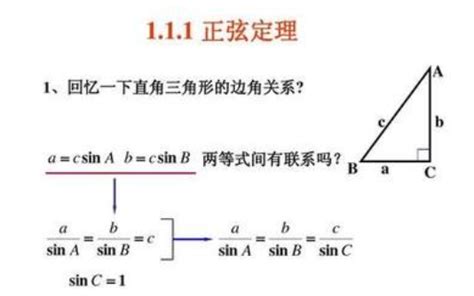 正弦定理与余弦定理的定义及解析新闻资讯11-24
正弦定理与余弦定理的定义及解析新闻资讯11-24 -
 揭秘:掌握数学精髓,三个不可或缺的中值定理公式详解新闻资讯11-08
揭秘:掌握数学精髓,三个不可或缺的中值定理公式详解新闻资讯11-08 -
 如何证明全等三角形的方法有哪些?新闻资讯11-05
如何证明全等三角形的方法有哪些?新闻资讯11-05










