如何证明全等三角形的方法有哪些?
全等三角形是几何学中的一个基本概念,指的是能够完全重合的两个三角形。在证明两个三角形是否全等时,我们需要借助一些明确的判定定理。以下是几种常用的全等三角形证明方法,涵盖了边边边(SSS)、边角边(SAS)、角边角(ASA)、角角边(AAS)和斜边直角边(HL)等五种主要判定方式。
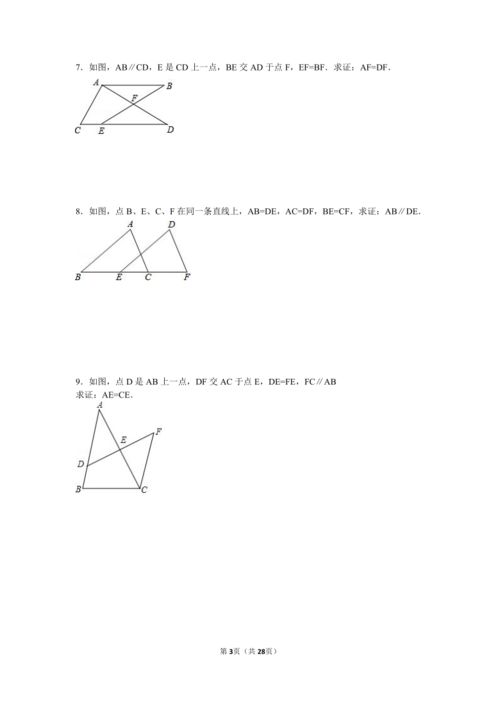
SSS(边边边)全等
SSS全等是指两个三角形的三边分别相等时,这两个三角形全等。这是最直接且容易理解的一种证明方法。

定义与示例:
假设三角形ABC和三角形DEF的三边分别相等,即AB=DE,BC=EF,AC=DF,则根据SSS全等定理,我们可以确定三角形ABC全等于三角形DEF。
证明过程:
1. 已知条件:AB=DE,BC=EF,AC=DF。
2. 构造辅助线(可选):为了更直观地理解,我们可以过三角形的顶点作高,例如过点A作AD⊥BC,过点D作DF⊥BE,延长AD和DF使其交于点G。
3. 推导角度相等:由于AB=DE,BC=EF,我们可以通过SAS(边角边)证明△ABC≌△DEF,从而得出∠BAC=∠EDF,∠ABC=∠DEF。
4. 进一步推导:由于AD⊥BC,DF⊥BE,则∠BAD=∠BDF=90°。在△AGD和△DFG中,因为AG=DG(同为AD的中垂线),∠BAD=∠BDF=90°,∠DAG=∠DFG(同为∠BAC的对应角),所以△AGD≌△DFG(SAS全等),从而得出AD=DF。
5. 总结:因为三角形ABC和三角形DEF在三条边上都相等,故△ABC≌△DEF。
SAS(边角边)全等
SAS全等是指两个三角形的两边及其夹角分别相等时,这两个三角形全等。
定义与示例:
假设三角形ABC和三角形DEF中,AB=DE,BC=EF,∠B=∠E,则根据SAS全等定理,我们可以确定三角形ABC全等于三角形DEF。
证明过程:
1. 已知条件:AB=DE,BC=EF,∠B=∠E。
2. 构造辅助线:以A、D两点为圆心,分别以AB、DE为半径作圆,则这两个圆会相交于一点G(因为AB=DE)。
3. 连接辅助线:连接AG,则△AGB和△DGE是等腰三角形。由于∠B=∠E,则∠AGB=∠DGE。
4. 推导边相等:由于AB=DE,BG=GE(等腰三角形的性质),所以△AGB≌△DGE(SAS全等),从而得出AG=DG。
5. 总结:在△ABC和△DEF中,因为AB=DE,∠B=∠E,AG=DG(由前面的推导得出),所以△ABC≌△DEF(SAS全等)。
ASA(角边角)全等
ASA全等是指两个三角形的两角及其夹边分别相等时,这两个三角形全等。
定义与示例:
假设三角形ABC和三角形DEF中,∠A=∠D,∠B=∠E,AB=DE,则根据ASA全等定理,我们可以确定三角形ABC全等于三角形DEF。
证明过程:
1. 已知条件:∠A=∠D,∠B=∠E,AB=DE。
2. 构造辅助线:以A、D两点为圆心,分别以AC、DE为半径作圆,则这两个圆会相交于一点G(因为AC=DE)。
3. 连接辅助线:连接AG,则△AGB和△DGE是等腰三角形。由于∠B=∠E,则∠AGB=∠DGE。
4. 推导边相等:由于AC=DE,BG=GE(等腰三角形的性质),所以△AGB≌△DGE(SAS全等),从而得出AG=DG。
5. 总结:在△ABC和△DEF中,因为∠A=∠D,∠B=∠E,AG=DG(由前面的推导得出),所以△ABC≌△DEF(ASA全等)。
AAS(角角边)全等
AAS全等是指两个三角形的两角及其中一个角的对边分别相等时,这两个三角形全等。
定义与示例:
假设三角形ABC和三角形DEF中,∠A=∠D,∠B=∠
- 上一篇: 完美可乐鸡翅的制作方法
- 下一篇: 蚯蚓主要以什么为食?
-
 全等三角形的判定方法新闻资讯11-05
全等三角形的判定方法新闻资讯11-05 -
 全等三角形的六种判定条件是什么?新闻资讯12-05
全等三角形的六种判定条件是什么?新闻资讯12-05 -
 掌握这几种技巧,轻松判断全等三角形!新闻资讯11-24
掌握这几种技巧,轻松判断全等三角形!新闻资讯11-24 -
 正四棱锥的明确定义解析新闻资讯10-28
正四棱锥的明确定义解析新闻资讯10-28 -
 中位线定理的证明方法新闻资讯11-26
中位线定理的证明方法新闻资讯11-26 -
 问答揭秘:如何轻松验证直角三角形斜边中线的独特定理?新闻资讯10-26
问答揭秘:如何轻松验证直角三角形斜边中线的独特定理?新闻资讯10-26












