正四棱锥的明确定义解析
正四棱锥,作为一种具有鲜明几何特征与广泛应用价值的立体图形,在几何学、工程学及建筑设计中占据着重要地位。本文将从定义、性质、度量关系及应用领域等方面,对正四棱锥进行全面而简洁的介绍,旨在提升读者的理解深度与阅读体验,同时兼顾搜索引擎的友好度。
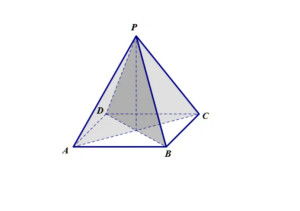
正四棱锥的定义
正四棱锥,顾名思义,是一种底面为正方形,侧面由四个全等的等腰三角形组成,且这些三角形共有一个顶点的棱锥。这一定义明确了正四棱锥的三个基本要素:底面(正方形)、侧面(四个全等的等腰三角形)以及顶点(这些三角形的公共顶点)。正四棱锥以其独特的形状和对称性,在几何学中展现出非凡的魅力。
性质解析
底面特征
正四棱锥的底面是一个正方形,这意味着它拥有四条等长的边和四个直角。正方形的这一特性,使得正四棱锥在底面结构上显得尤为规整和稳定。
侧面与侧棱
正四棱锥的侧面由四个全等的等腰三角形构成,这些三角形的底边正是正方形的四条边,而它们的腰则是连接顶点与底面各顶点的侧棱。由于侧棱长度相等且均为等腰三角形的腰,正四棱锥的侧面展现出了高度的对称性。此外,这些侧棱还共同指向顶点,形成了一个尖锐的锥顶,增强了棱锥的立体感。
顶点与对称性
所有侧面和侧棱的公共交点即为正四棱锥的顶点。顶点在底面的投影恰好是底面的中心,这一性质进一步强化了正四棱锥的对称美。沿着过顶点和底面中心的垂直轴,正四棱锥具有四棱对称性,即无论从哪个方向观察,其外观都保持一致。
度量关系
在度量关系上,正四棱锥的高是顶点到底面中心的距离,这一高度对于计算棱锥的体积至关重要。体积的计算公式为底面积乘以三分之一的高,即$V = \frac{1}{3} \times \text{底面积} \times \text{高}$。此外,正四棱锥的侧面面积也易于计算,每个侧面面积等于底面边长乘以一半的侧棱斜率(也即等腰三角形的高),四者之和即为总侧面面积。
应用领域
正四棱锥的独特性质使其在多个领域得到了广泛应用。
工程设计与建筑
在工程设计领域,正四棱锥常被用作支撑结构。其稳定的底面结构和尖锐的锥顶,使得正四棱锥能够承受较大的压力和应力,从而成为建筑物、桥梁等结构中的重要组成部分。此外,正四棱锥的对称性还使得其设计更加美观和谐,提升了建筑的整体视觉效果。
容器设计
在容器设计方面,正四棱锥也展现出其独特的优势。例如,漏斗和料斗等容器常采用正四棱锥的形状设计。这种设计不仅便于物料的导入和导出,还能够有效地减少物料的残留和浪费。同时,正四棱锥的侧面还具有一定的倾斜度,有助于物料的顺畅流动。
装饰品与艺术
在装饰品和艺术领域,正四棱锥同样受到青睐。灯罩、花瓶等装饰品常采用正四棱锥的形状设计,以展现其独特的几何美感和空间感。正四棱锥的简洁线条和对称结构,使得这些装饰品在视觉上更加富有层次感和动感。
结语
综上所述,正四棱锥作为一种具有鲜明几何特征和广泛应用价值的立体图形,在几何学、工程学及建筑设计中发挥着重要作用。其定义清晰、性质独特、度量关系明确,使得正四棱锥在多个领域都展现出了强大的生命力和创造力。未来,随着科技的不断进步和设计的不断创新,正四棱锥的应用领域还将进一步拓展和深化。
- 上一篇: 揭秘!'employees'的正确发音,你读对了吗?
- 下一篇: 揭秘哇嘎:这款应用究竟有何神奇用途?
-
 正四棱锥的特性和属性解析新闻资讯11-24
正四棱锥的特性和属性解析新闻资讯11-24 -
 揭秘:正四棱锥的准确定义是什么?新闻资讯11-08
揭秘:正四棱锥的准确定义是什么?新闻资讯11-08 -
 想知道如何轻松画出正四棱锥?一图解析,让你秒变绘图达人!新闻资讯10-28
想知道如何轻松画出正四棱锥?一图解析,让你秒变绘图达人!新闻资讯10-28 -
 如何用卡纸制作一个简单的正四棱锥?新闻资讯11-08
如何用卡纸制作一个简单的正四棱锥?新闻资讯11-08 -
 掌握素描精髓:轻松学会四棱锥的绘制技巧新闻资讯11-08
掌握素描精髓:轻松学会四棱锥的绘制技巧新闻资讯11-08 -
 掌握技巧:轻松绘制四棱锥立体图新闻资讯11-08
掌握技巧:轻松绘制四棱锥立体图新闻资讯11-08












