揭秘:正四棱锥的准确定义是什么?
正四棱锥是一种具有特定几何特性的三维多面体,它在几何学、工程学、建筑学等多个领域都有着广泛的应用。以下是对正四棱锥的详细介绍,旨在通过清晰的结构和简洁的语言,让读者全面了解这一几何形状。
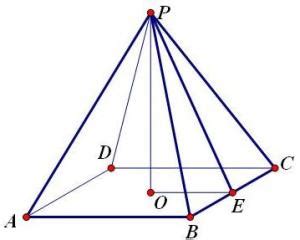
正四棱锥的定义始于其底面与侧面的特征。具体来说,正四棱锥的底面是一个正方形,这一特性决定了其名称中的“四棱”部分。与此同时,它的侧面由四个全等的等腰三角形构成,这四个三角形不仅形状相同,而且有一个公共的顶点,这个点即为正四棱锥的顶点。进一步地,这个顶点在底面的投影恰好位于正方形的中心,这一特征保证了正四棱锥的对称性和稳定性。

在了解正四棱锥的基本定义后,我们可以深入探讨其几何性质。首先,由于正四棱锥的侧棱相等,各侧面(等腰三角形)的底边上的高也相等,这个高通常被称为正棱锥的斜高。其次,正四棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,这一性质为计算正四棱锥的相关参数提供了便利。此外,正四棱锥的侧棱与底面所成的角都相等,侧面与底面所成的二面角也都相等,这些性质进一步增强了正四棱锥的对称性和美感。
在体积计算方面,正四棱锥遵循所有椎体(圆锥或棱锥)共同的体积公式,即三分之一底面积乘以高。这里的底面积指的是正四棱锥底面的正方形面积,高则是从顶点到底面的垂直距离。在计算过程中,需要确保底面积和高的单位一致,以避免计算结果出现错误。
除了基本的几何性质和体积计算外,正四棱锥的展开图也是了解其结构的重要工具。展开图是将正四棱锥的各个面展开到同一平面上的图形,它有助于我们更直观地理解正四棱锥的构造和各个面之间的关系。通过观察展开图,我们可以清晰地看到正四棱锥的底面、侧面以及它们之间的连接关系。
在实际应用中,正四棱锥因其独特的几何特性而具有广泛的应用价值。在建筑领域,正四棱锥可以用作建筑物或桥梁的支撑结构,其稳定的结构和良好的受力性能使其成为工程设计的优选。此外,正四棱锥还可以用作容器,如漏斗、料斗等,其形状便于物料的流动和储存。在装饰领域,正四棱锥也因其独特的造型和美感而被广泛应用于灯罩、花瓶等装饰品的制作中。
值得注意的是,正四棱锥只是四棱锥的一种特殊情况。四棱锥是指由四个三角形和一个四边形构成的空间封闭图形,其结构可以看作是由长方体结构演变而来。根据底面形状和顶点位置的不同,四棱锥可以分为正四棱锥和斜四棱锥等多种类型。其中,正四棱锥具有最高的对称性和稳定性,因此在实际应用中更为常见。
在进一步了解正四棱锥的过程中,我们还可以探讨其与其他几何形状的关系。例如,正四棱锥可以看作是圆锥的一种特殊情况,即当圆锥的底面变为正方形时,就形成了正四棱锥。这种关系有助于我们更深入地理解正四棱锥的几何特性和计算方法。
此外,正四棱锥在几何学中的研究也具有重要的理论价值。通过对正四棱锥的研究,我们可以更深入地理解多面体的构造和性质,进一步拓展几何学的应用领域。同时,正四棱锥也是数学教育和科学研究中的重要内容之一,它有助于学生培养空间想象力和几何直觉能力。
总的来说,正四棱锥是一种具有独特几何特性和广泛应用价值的三维多面体。通过对其定义、几何性质、体积计算以及实际应用等方面的介绍,我们可以更全面地了解这一几何形状。正四棱锥不仅在数学教育和科学研究中扮演着重要角色,还在建筑、工程、装饰等多个领域发挥着重要作用。因此,深入研究正四棱锥的特性和应用对于我们理解几何学的基本原理和拓展其应用领域具有重要意义。
最后,需要强调的是,虽然正四棱锥具有独特的几何特性和广泛的应用价值,但在实际应用中仍需根据具体情况进行选择和调整。例如,在建筑设计中,需要综合考虑结构稳定性、施工难度和成本效益等因素来确定是否使用正四棱锥作为支撑结构。同样地,在装饰设计中,也需要根据设计风格和空间布局等因素来选择合适的正四棱锥造型和尺寸。因此,在实际应用中,我们需要灵活运用正四棱锥的特性和原理,以实现最佳的设计效果和应用价值。
-
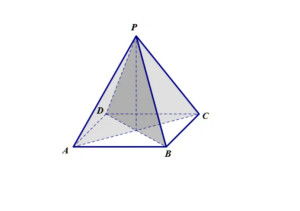 正四棱锥的明确定义解析新闻资讯10-28
正四棱锥的明确定义解析新闻资讯10-28 -
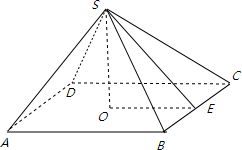 正四棱锥的特性和属性解析新闻资讯11-24
正四棱锥的特性和属性解析新闻资讯11-24 -
 如何用卡纸制作一个简单的正四棱锥?新闻资讯11-08
如何用卡纸制作一个简单的正四棱锥?新闻资讯11-08 -
 想知道如何轻松画出正四棱锥?一图解析,让你秒变绘图达人!新闻资讯10-28
想知道如何轻松画出正四棱锥?一图解析,让你秒变绘图达人!新闻资讯10-28 -
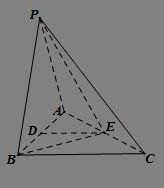 掌握技巧:轻松绘制四棱锥立体图新闻资讯11-08
掌握技巧:轻松绘制四棱锥立体图新闻资讯11-08 -
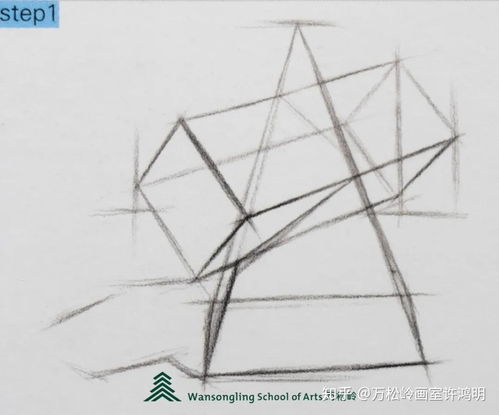 掌握素描精髓:轻松学会四棱锥的绘制技巧新闻资讯11-08
掌握素描精髓:轻松学会四棱锥的绘制技巧新闻资讯11-08












