正四棱锥的特性和属性解析
正四棱锥的性质深度解析
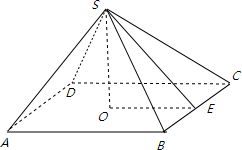
正四棱锥作为一种常见的立体几何图形,在几何学、工程学以及日常生活中都有着广泛的应用。其独特的形状和性质使得它成为研究几何性质、进行空间分析的重要对象。本文将详细解析正四棱锥的性质,帮助读者更好地理解和应用这一几何体。

一、定义与基本构造
正四棱锥是指底面为正方形,顶点位于底面中心垂直上方,且顶点与底面四边距离相等的锥体。设正四棱锥的底面边长为a,斜高(顶点到底面一边的垂直距离)为h',高(顶点到底面的垂直距离)为h。
二、表面积与体积
1. 表面积
正四棱锥的表面积由底面和四个侧面组成。底面是一个正方形,面积为a²。四个侧面都是等腰三角形,面积均为1/2ah'。因此,正四棱锥的总表面积为:
S = a² + 4 × (1/2ah') = a² + 2ah'
利用勾股定理,斜高h'可以表示为:
h' = √(h² + (a/2)²)
代入上式,得到正四棱锥的表面积公式为:
S = a² + 2a√(h² + (a/2)²)
2. 体积
正四棱锥的体积可以通过底面积与高来计算。底面积为a²,高为h,因此体积V为:
V = (1/3)a²h
这个公式直接体现了锥体体积的一般性质,即体积等于底面积乘以高再除以3。
三、顶点与棱的性质
1. 顶点性质
正四棱锥的顶点位于底面中心的正上方,与底面四边的距离相等。这意味着顶点到底面任意一点的距离都是h,保证了锥体的对称性和均匀性。
2. 棱的性质
正四棱锥有4条侧棱和4条底棱。侧棱连接顶点与底面四边的中点,长度均为斜高h'。底棱是底面正方形的边,长度为a。所有棱的长度相等且互相垂直,使得正四棱锥具有极强的结构稳定性和对称性。
四、角度与垂直关系
1. 角度关系
在正四棱锥中,顶点与底面任意两点的连线形成的夹角是等腰三角形的顶角。由于底面是正方形,这个夹角在底面投影上形成的是正方形的对角线夹角,即45°或135°的补角。但需要注意的是,这里的45°或135°是底面投影的角度,实际的三维空间中角度会随斜高h'和底面边长a的变化而变化。
2. 垂直关系
正四棱锥的顶点到底面是垂直的,这意味着顶点与底面任意一点连线的线段都与底面垂直。此外,由于底面是正方形,其四边互相垂直,因此正四棱锥的四个侧面也都是与底面垂直的平面。
五、对称性
正四棱锥具有高度的对称性。首先,它关于底面中心垂直轴对称;其次,它还关于底面两条对角线的垂直平面对称。这种对称性不仅使得正四棱锥在视觉上更加美观,也使其在力学性能和结构稳定性上表现出色。
六、投影与截面
1. 投影
正四棱锥在不同方向上的投影具有不同的形状。当光线垂直于底面时,投影是一个正方形;当光线与底面成一定角度时,投影会变成一个椭圆或菱形。这些投影形状的变化反映了正四棱锥在空间中的立体感和动态性。
2. 截面
正四棱锥的截面可以是多种形状,取决于截面平面的方向和位置。常见的截面包括正方形、三角形、菱形和椭圆等。这些截面形状的变化不仅丰富了正四棱锥的几何性质,也为其在工程学和日常生活中的应用提供了更多的可能性。
七、正四棱锥的展开图
正四棱锥的展开图是将其各个面展开到同一个平面上得到的图形。它由底面正方形和四个等腰三角形组成。这些三角形通过共享一条边(即底面正方形的一边)相互连接。展开图不仅有助于我们更直观地理解正四棱锥的结构和形状,还在制作模型、设计图案等方面有着广泛的应用。
八、正四棱锥与其他几何体的关系
1. 与正方体的关系
正四棱锥与正方体有着密切的关系。如果将正四棱锥的顶点向下平移至与底面重合,并扩展为一个与底面相同的正方形平面,那么得到的立体图形就是一个正方体。因此,正四棱锥可以看作是正方体被截去一个顶角后得到的几何体。
2. 与三棱锥的关系
正四棱锥可以看作是由四个全等的等腰直角三角形三棱锥组成的复合体。这四个三棱锥共享一个顶点(即正四棱锥的顶点),并且它们的底面分别位于正四棱锥的四个侧面上。这种关系使得正四棱锥在几何性质和计算方法上与三棱锥有着一定的联系和区别。
九、正四棱锥的实际应用
正四棱锥在实际生活中有着广泛的应用。例如,在建筑设计中,正四棱锥的形状可以被用作屋顶或塔楼的造型元素,增加建筑的艺术感和空间感;在工程学中,正四棱锥的结构稳定性和对称性使其成为制造机器零件、设计支架等的重要选择;在数学教育中,正四棱锥也是教授立体几何、培养空间思维能力的重要工具之一。
综上所述,正四棱锥作为一种常见的立体几何图形,具有丰富的性质和广泛的应用价值。通过对其表面积、体积、顶点与棱的性质、角度与垂直关系、对称性、投影与截面等方面的深入解析,我们可以更好地理解和应用这一几何体。同时,正四棱锥与其他几何体的关系以及其在实际生活中的应用也为我们提供了更多的思考和探索空间。
- 上一篇: 清蒸梭子蟹的制作方法是什么?
- 下一篇: 快速掌握:如何高效联系QQ腾讯人工在线客服
-
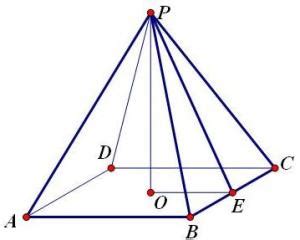 揭秘:正四棱锥的准确定义是什么?新闻资讯11-08
揭秘:正四棱锥的准确定义是什么?新闻资讯11-08 -
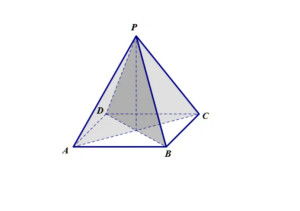 正四棱锥的明确定义解析新闻资讯10-28
正四棱锥的明确定义解析新闻资讯10-28 -
 想知道如何轻松画出正四棱锥?一图解析,让你秒变绘图达人!新闻资讯10-28
想知道如何轻松画出正四棱锥?一图解析,让你秒变绘图达人!新闻资讯10-28 -
 如何用卡纸制作一个简单的正四棱锥?新闻资讯11-08
如何用卡纸制作一个简单的正四棱锥?新闻资讯11-08 -
 掌握素描精髓:轻松学会四棱锥的绘制技巧新闻资讯11-08
掌握素描精髓:轻松学会四棱锥的绘制技巧新闻资讯11-08 -
 掌握技巧:轻松绘制四棱锥立体图新闻资讯11-08
掌握技巧:轻松绘制四棱锥立体图新闻资讯11-08












