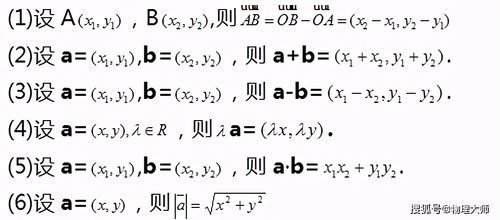揭秘平行线的魔力:线段比例分割的奥秘
在数学的浩瀚宇宙中,平行线与线段之间的关系一直是几何学研究的重要内容。其中,“平行线分线段成比例定理”作为这一领域的基本定理之一,不仅揭示了平行线在分割线段时所遵循的规律,也为后续学习更复杂的几何定理和证明提供了坚实的基础。本文将围绕平行线分线段成比例定理展开,通过深入探讨其定义、性质、证明方法以及应用实例,带领读者走进这一几何定理的奇妙世界。
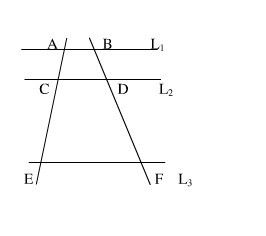
平行线分线段成比例定理的核心在于描述了两条平行线被第三条直线(称为横截线)所截时,它们将横截线分割成的线段之间的比例关系。具体来说,如果两条平行线a和b被一条横截线c所截,那么c在a和b上分别截得的线段长度之比是相等的。这个定理在几何学中具有重要意义,它为我们提供了一种利用平行线来求解线段比例的方法,同时也为证明其他几何定理提供了有力的工具。
在深入探讨这个定理之前,我们需要明确几个基本概念。首先,平行线是指在同一平面内,永不相交的两条直线。它们之间的距离始终保持不变,这一性质是平行线在几何学中发挥重要作用的基础。其次,线段是直线的一部分,由两个端点确定。在平行线分线段成比例定理中,我们关注的是被平行线分割的线段之间的比例关系。
现在,让我们来详细探讨平行线分线段成比例定理的性质。该定理不仅适用于两条平行线被一条横截线所截的情况,还适用于更一般的情形,即当有多条平行线被同一条横截线所截时,它们将横截线分割成的线段之间的比例关系仍然成立。这一性质使得平行线分线段成比例定理在解决复杂几何问题时具有更高的灵活性和实用性。
接下来,我们来分析平行线分线段成比例定理的证明方法。证明的关键在于利用平行线的性质来推导出线段之间的比例关系。具体来说,我们可以通过构造辅助线(如过某一线段的一个端点作平行于另一条平行线的直线)来构造出相似三角形,从而利用相似三角形的性质(对应边之间的比例相等)来证明线段之间的比例关系。此外,还可以利用向量的线性关系、解析几何中的坐标变换等方法来证明该定理。这些证明方法不仅展示了平行线分线段成比例定理的多样性,也为我们提供了不同的思考角度和解题策略。
在实际应用中,平行线分线段成比例定理具有广泛的应用价值。首先,它可以用于求解线段长度问题。当已知一些线段的长度和它们之间的比例关系时,我们可以利用该定理来求解未知线段的长度。其次,它可以用于证明其他几何定理。例如,在证明三角形内角和定理时,我们可以利用平行线分线段成比例定理来推导出三角形内角和为180度的结论。此外,该定理还可以用于解决一些与面积相关的问题。当已知一些图形的面积和它们之间的比例关系时,我们可以利用该定理来求解未知图形的面积。
在具体的应用实例中,我们可以看到平行线分线段成比例定理在解决实际问题中的威力。例如,在建筑设计领域,工程师可以利用该定理来计算建筑物的高度、宽度等尺寸;在地理测量领域,测量人员可以利用该定理来测量地形地貌的高度差、距离等参数;在图形设计领域,设计师可以利用该定理来设计具有美感的图形和图案。这些应用实例不仅展示了平行线分线段成比例定理在解决实际问题中的重要作用,也为我们提供了更多的思考角度和应用场景。
值得注意的是,虽然平行线分线段成比例定理在几何学中发挥着重要作用,但它并不是孤立存在的。在几何学的知识体系中,它与其他几何定理和性质之间存在着密切的联系和互动。例如,它与相似三角形的性质、三角形的内角和定理、勾股定理等定理之间存在着紧密的联系。这些联系不仅为我们提供了更多的解题方法和策略,也为我们更深入地理解几何学提供了更广阔的视野和更深入的思考。
此外,平行线分线段成比例定理在教育学领域也具有重要意义。作为教师,我们可以利用该定理来培养学生的几何思维和空间想象能力。通过引导学生观察、分析、证明该定理的过程,我们可以帮助他们掌握几何学的基本方法和技巧,提高他们的数学素养和解决问题的能力。同时,我们还可以将平行线分线段成比例定理与其他学科相结合,如物理、化学等,从而拓展学生的知识面和视野。
综上所述,平行线分线段成比例定理作为几何学的基本定理之一,在揭示平行线与线段之间关系的同时,也为我们提供了一种求解线段比例问题的方法。通过深入探讨其定义、性质、证明方法以及应用实例,我们可以更好地理解和应用这一几何定理。在未来的学习和研究中,我们将继续探索平行线分线段成比例定理的更多应用和价值,为数学和几何学的发展贡献更多的智慧和力量。
- 上一篇: 揭秘:解锁恶魔少女‘真实之眼’的神秘方法
- 下一篇: 珠宝玉石的鉴定方法有哪些?
-
 揭秘梯形面积计算的奥秘新闻资讯10-30
揭秘梯形面积计算的奥秘新闻资讯10-30 -
 向量平行的判定公式是什么新闻资讯11-03
向量平行的判定公式是什么新闻资讯11-03 -
 揭秘!圆台侧面积公式的推导奥秘,你也能轻松掌握新闻资讯10-25
揭秘!圆台侧面积公式的推导奥秘,你也能轻松掌握新闻资讯10-25 -
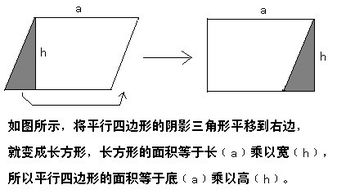 平行四边形面积计算公式详解新闻资讯11-24
平行四边形面积计算公式详解新闻资讯11-24 -
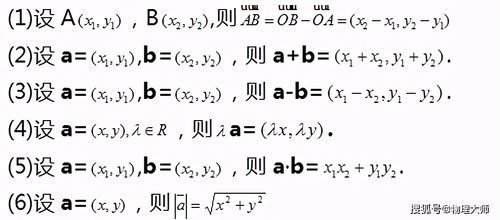 向量平行与垂直的公式是什么?新闻资讯11-05
向量平行与垂直的公式是什么?新闻资讯11-05 -
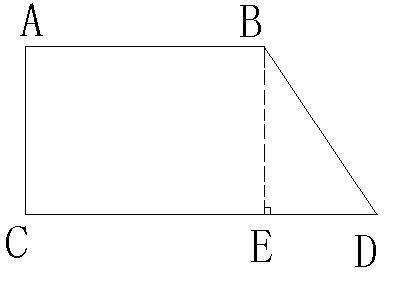 揭秘梯形面积计算的奥秘公式新闻资讯10-30
揭秘梯形面积计算的奥秘公式新闻资讯10-30