揭秘！圆台侧面积公式的推导奥秘，你也能轻松掌握

在几何学中，圆台是一个上底面和下底面都是圆形且互相平行的立体图形，其侧面则是连接这两个圆面的曲面部分。当我们需要计算圆台的侧面积时，一个简洁而有效的公式便显得尤为重要。那么，圆台的侧面积公式是如何推导出来的呢？下面，我们就来一步步揭开这个公式的神秘面纱。

圆台的基本认识

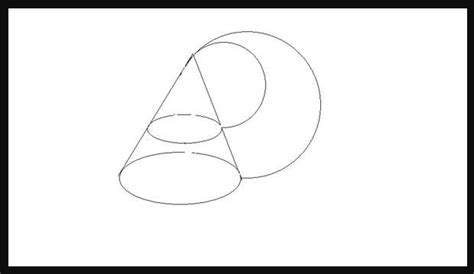
首先，我们需要明确圆台的一些基本属性。圆台有两个底面，分别称为上底和下底，它们的半径一般不相等，分别记为$r$（上底半径）和$R$（下底半径）。另外，圆台还有一条特殊的线段，叫做母线，它是连接上底和下底边缘任意两点的直线段，其长度记为$l$。

侧面展开图的思考

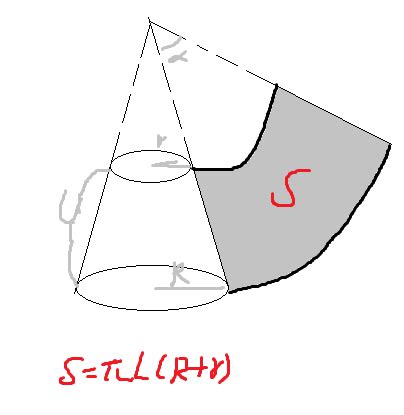
要计算圆台的侧面积，一个直观的想法是将它的侧面展开。想象一下，如果我们把圆台沿着母线剪开，并将其侧面展开到平面上，我们会得到一个扇形（或环形的一部分）形状的图形。这个扇形的半径就等于圆台的母线长$l$，而它的弧长则是由圆台上下底面的周长共同构成的。

扇形面积的启示

扇形面积的计算公式是：$S = \frac{1}{2} \times \text{弧长} \times \text{半径}$。在圆台侧面展开成扇形的情况下，扇形的弧长可以看作是圆台上下底面周长之和的一半（因为扇形的弧长实际上是从圆台侧面截取出来的一部分，而圆台的侧面是由整个环形曲面组成的）。

圆台上下底面的周长分别是$2\pi r$和$2\pi R$，所以它们的和是$2\pi r + 2\pi R = 2\pi(r + R)$。但是，我们需要注意，这个总周长是对应整个环形曲面的，而扇形只占据了其中的一部分。因此，在计算扇形弧长时，我们应该用总周长的一半乘以一个系数（这个系数实际上与扇形的具体形状有关，但在推导中我们可以通过其他方式消去它）。不过，为了简化问题，我们可以暂时假设扇形弧长就等于圆台上下底面周长之和的一半，即$\pi(r + R)$。

推导过程

接下来，我们利用扇形面积公式来推导圆台的侧面积公式。将扇形的弧长$\pi(r + R)$和半径$l$代入扇形面积公式，得到：

$$S_{\text{侧}} = \frac{1}{2} \times \pi(r + R) \times l = \pi l(r + R)$$

这个公式就是圆台侧面积的基本形式。它告诉我们，圆台的侧面积与其母线长$l$以及上下底面半径之和$r + R$成正比。

另一种视角的推导

除了直接从扇形面积出发推导外，我们还可以通过考虑圆台与大圆锥和小圆锥的关系来推导侧面积公式。想象一个底面半径为$R$、高为$H$的大圆锥，以及一个底面半径为$r$、高为$h'$的小圆锥。如果我们从大圆锥中截去这个小圆锥，剩下的部分就是一个圆台。

圆台的侧面积可以看作是大圆锥侧面积减去小圆锥侧面积。大圆锥的侧面积公式是$\pi RL$（其中$L$是大圆锥的母线长，可以通过勾股定理求得，即$L = \sqrt{R^2 + H^2}$），小圆锥的侧面积公式是$\pi rl'$（其中$l'$是小圆锥的母线长，同样可以通过勾股定理求得，但在这里我们不需要具体求出它的值，因为我们会通过比例关系消去它）。

然而，这里有一个问题：我们并不知道小圆锥的高$h'$是多少，因此无法直接求出$l'$。但幸运的是，我们可以通过比例关系来绕过这个障碍。由于大圆锥和小圆锥是相似的，所以它们的母线长之比等于底面半径之比，即$r:R = l':L$。解这个比例关系，我们可以得到$l' = \frac{rL}{R}$。

但请注意，这里的$L$并不是我们要求的圆台的母线长$l$。实际上，圆台的母线长$l$等于大圆锥的母线长$L$减去小圆锥的高对应的在圆锥侧面上的长度（这个长度并不等于小圆锥的高$h'$，而是与$h'$成比例的一个量）。但在这里，我们可以直接利用已知的$r$、$R$和$l$来推导公式，而不需要显式地求出$L$和$l'$。

更直接的方法是，我们注意到圆台的侧面可以看作是由无数个小扇形组成的（这些小扇形是圆台侧面在极坐标系下的微小部分），每个小扇形的面积都可以用类似的扇形面积公式来计算，并