圆台侧面积计算公式详解
圆台的侧面积计算是几何学中的一个重要问题,它涉及到空间几何的形状、面积和体积等方面的知识。对于许多从事工程设计、建筑、制造等领域的专业人士来说,理解和掌握圆台侧面积的计算方法至关重要。本文将从圆台的基本定义出发,逐步推导圆台的侧面积公式,并通过实例加以说明,以帮助读者更好地掌握这一知识点。

圆台,又称圆锥台,是由两个平行且相等的圆面(称为上底面和下底面)以及连接这两个圆面的侧面所围成的几何体。与圆锥类似,圆台也具有一个顶点,称为圆台的顶点,该顶点位于上底面圆的上方,并与下底面圆的圆心通过一条直线相连,这条直线称为圆台的高。圆台的高、上底面半径和下底面半径是圆台的基本参数,它们决定了圆台的形状和大小。

在计算圆台的侧面积之前,我们先回顾一下圆锥的侧面积计算公式。圆锥的侧面积公式为:侧面积 = πrl,其中r为圆锥底面的半径,l为圆锥的母线长。母线是连接圆锥顶点与底面圆上任一点的线段。这一公式的推导过程基于圆锥的侧面展开图是一个扇形的事实,扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线长。
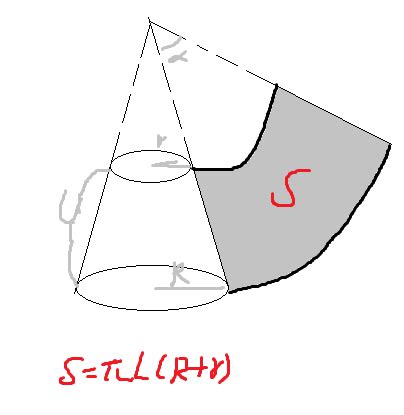
圆台的侧面积计算过程与圆锥类似,但稍微复杂一些。圆台的侧面展开图是一个圆环的一部分,这个圆环的内外圆周长分别等于圆台的上底面和下底面的周长,而圆环的半径则与圆台的母线长有关。为了推导圆台的侧面积公式,我们需要先求出圆台的母线长。
圆台的母线长可以通过勾股定理求得。设圆台的高为h,上底面半径为r,下底面半径为R,则母线长l可以通过以下公式计算:l = √[(R - r)^2 + h^2]。这个公式的推导过程基于圆台的侧面视图是一个直角梯形的事实,其中直角梯形的上底和下底分别等于圆台的上底面半径和下底面半径,而直角梯形的高等于圆台的高。通过勾股定理,我们可以求出直角梯形的斜边,即圆台的母线长。
有了圆台的母线长,我们就可以计算圆台的侧面积了。圆台的侧面积公式为:侧面积 = π(R + r)l,其中R为下底面半径,r为上底面半径,l为母线长。这个公式的推导过程基于圆台的侧面展开图是一个圆环的一部分的事实。圆环的内外圆周长分别等于圆台的上底面和下底面的周长,即2πr和2πR,而圆环的“宽”则与圆台的母线长有关。由于圆环展开后是一个矩形(其长等于圆环的内外圆周长之差的一半,即π(R - r),宽等于圆台的母线长l),因此圆台的侧面积等于这个矩形的面积,即π(R + r)l(注意这里R + r是矩形长的两倍除以2π后的结果,与l相乘得到面积)。
为了加深理解,我们可以通过一个具体的例子来计算圆台的侧面积。假设有一个圆台,其高h为10厘米,上底面半径r为5厘米,下底面半径R为10厘米。首先,我们计算圆台的母线长l:l = √[(R - r)^2 + h^2] = √[(10 - 5)^2 + 10^2] = √[25 + 100] = √125 = 5√5厘米。然后,我们将R、r和l代入圆台的侧面积公式中计算侧面积:侧面积 = π(R + r)l = π(10 + 5) × 5√5 = 15π × 5√5 = 75√5π平方厘米(这里我们可以将π取近似值3.14进行计算,得到侧面积的近似值)。
圆台的侧面积计算不仅在数学和物理学中有广泛应用,在工程设计和制造中也具有重要意义。例如,在设计一个漏斗或圆锥形的容器时,我们需要知道其侧面积以确定所需的材料量。同样地,在计算一个圆台形的建筑物的表面积时,我们也需要知道其侧面积以进行准确的造价估算。
此外,圆台的侧面积还与一些实际问题密切相关。例如,在求解一个圆台形的水池能够装多少水时,我们需要知道其体积。而圆台的体积公式(V = (1/3)πh(R^2 + r^2 + Rr))中就包含了侧面积的相关元素(虽然侧面积本身并不直接等于体积)。同样地,在求解一个圆台形的物体在液体中的浮力时,我们也需要知道其表面积(包括侧面积和底面积)以确定其排开液体的体积和重量。
综上所述,圆台的侧面积计算是几何学中的一个重要问题。通过理解和掌握圆台的基本定义、母线长的计算方法和侧面积公式,我们可以更好地解决与圆台相关的实际问题。同时,圆台的侧面积计算也为我们提供了解决类似空间几何问题的思路和方法,帮助我们更好地理解和应用几何学知识。
- 上一篇: gonna是什么意思?
- 下一篇: 美国与中国时差是多少
-
 揭秘!圆台侧面积计算公式大公开,你了解多少?新闻资讯10-25
揭秘!圆台侧面积计算公式大公开,你了解多少?新闻资讯10-25 -
 揭秘!圆台侧面积公式的推导奥秘,你也能轻松掌握新闻资讯10-25
揭秘!圆台侧面积公式的推导奥秘,你也能轻松掌握新闻资讯10-25 -
 圆柱的侧面积计算公式及详解新闻资讯10-28
圆柱的侧面积计算公式及详解新闻资讯10-28 -
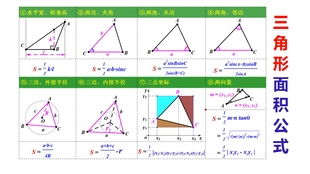 三角形面积计算公式详解新闻资讯11-25
三角形面积计算公式详解新闻资讯11-25 -
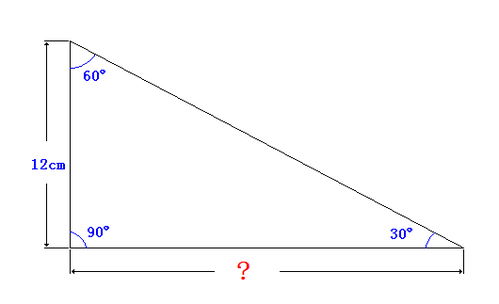 直角三角形面积计算公式详解新闻资讯10-31
直角三角形面积计算公式详解新闻资讯10-31 -
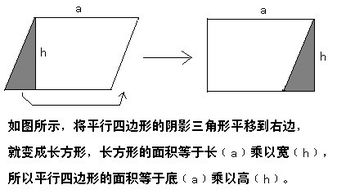 平行四边形面积计算公式详解新闻资讯11-24
平行四边形面积计算公式详解新闻资讯11-24












