初中三角形知识大全:定理、公理与定义详解
初中的三角形的定理、公理和定义

三角形是初中数学中的重要内容,它不仅是几何学的基础,还在代数、三角函数等多个领域有广泛应用。在初中阶段,我们会接触到三角形的各种定理、公理和定义,这些内容对于后续的学习和理解都至关重要。接下来,让我们一起回顾和探讨一下初中涉及的三角形的定理、公理和定义。

首先,我们来看看三角形的定义。三角形是由三条不在同一条直线上的线段首尾顺次连接所组成的平面图形。换句话说,三角形有三个顶点、三条边和三个内角。这三个内角的和总是等于180度,这是三角形内角和定理,也是我们在学习三角形时首先要掌握的基础知识。
接下来,我们来看看三角形的分类。根据边长,三角形可以分为等边三角形、等腰三角形和不等边三角形。等边三角形的三条边都相等,三个内角也都是60度;等腰三角形有两条边相等,且这两个边对应的两个内角也相等;不等边三角形的三条边各不相等,三个内角也没有相等的。根据内角的大小,三角形还可以分为锐角三角形、直角三角形和钝角三角形。锐角三角形的三个内角都小于90度;直角三角形有一个内角等于90度;钝角三角形有一个内角大于90度。
在三角形的边和角的关系上,有几个重要的定理。首先是三角形的两边之和大于第三边定理,也就是说,对于三角形中的任意两边,它们的和总是大于第三边。这个定理不仅给出了构成三角形的必要条件,还可以用来判断三条线段是否能构成三角形。另外,三角形的两边之差小于第三边定理也是类似的,即三角形中的任意两边之差总是小于第三边。
三角形的角平分线定理也是我们需要掌握的内容。如果一个点在三角形的一条边上,并且它将这条边所对的角平分,那么这个点就是这条角的平分线与对边的交点,且这条角平分线将对边分为两段,其中一段与这个点到顶点的连线构成的三角形与原三角形相似,并且它们的对应边之间的比例是相等的。这个定理在证明和计算中都有广泛的应用。
在三角形的中线定理中,三角形的中线是连接一个顶点和它所对边的中点的线段。中线定理告诉我们,三角形的三条中线总是相交于一点,并且这一点将中线分为两段,其中一段是另一段的2倍。此外,三条中线还将三角形分为面积相等的6个小三角形。
三角形的垂线定理和高也是重要的概念。三角形的垂线是从一个顶点垂直于它所对边或对边的延长线的线段,这条垂线与对边或对边的延长线的交点称为垂足。而三角形的高则是从三角形的一个顶点垂直到它的对边或对边的延长线,并且连接这个顶点和垂足的线段。三角形的三条高所在的直线总是相交于一点,这个点称为三角形的垂心。在直角三角形中,高的概念与直角边和斜边有关,斜边上的高就是从直角顶点垂直到斜边并连接垂足和直角顶点的线段。
除了这些定理,三角形的全等判定也是初中数学中的重点。三角形的全等是指两个三角形的三边和三角都分别相等。判定两个三角形全等的方法有多种,包括SSS(边边边)全等、SAS(边角边)全等、ASA(角边角)全等、AAS(角角边)全等和RHS(直角、斜边、边)全等。SSS全等是指两个三角形的三边分别相等;SAS全等是指两个三角形中有两边相等,并且这两边所对的角也相等;ASA全等是指两个三角形中有两角相等,并且这两角所夹的边也相等;AAS全等是指两个三角形中有两角相等,并且这两个角所夹的一边的对边也相等;RHS全等则是专门用于直角三角形,它要求两个直角三角形的一个直角相等,斜边相等,以及一条直角边也相等。
在三角形的面积计算上,我们也有相应的公式。对于任意三角形,如果已知它的底和高,那么它的面积就是底与高的乘积的一半。这个公式在解决实际问题时非常有用,比如计算土地面积、房屋面积等。此外,对于直角三角形,我们还可以通过勾股定理来计算面积,即直角三角形的面积等于两条直角边的乘积的一半。勾股定理是指在一个直角三角形中,直角边的平方和等于斜边的平方,即a²+b²=c²,其中a和b是直角边,c是斜边。
最后,我们来看看三角形的外角和内角的关系。三角形的外角是指三角形中任意一边所对的角的外角,也就是这条边所延长线与另一条边所夹的角。三角形的外角定理告诉我们,一个三角形的一个外角等于与它不相邻的两个内角的和。这个定理在证明和计算中都非常有用,可以帮助我们简化复杂的几何问题。
以上就是初中阶段关于三角形的定理、公理和定义的主要内容。这些知识点不仅在数学学科内部有着广泛的应用,而且在其他学科和现实生活中也有着重要的价值。通过深入理解和掌握这些定理、公理和定义,我们可以更好地解决几何问题,提高
- 上一篇: 雁栖湖畔,畅游秘境:详尽游玩攻略
- 下一篇: 如何轻松查询成绩
-
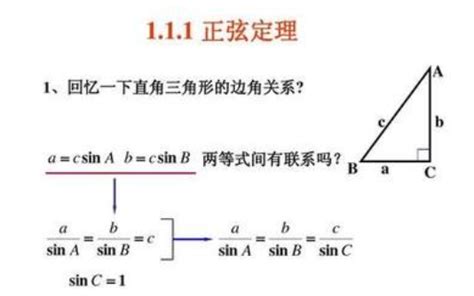 正弦定理与余弦定理的定义及解析新闻资讯11-24
正弦定理与余弦定理的定义及解析新闻资讯11-24 -
 正弦定理和余弦定理分别是什么?新闻资讯11-09
正弦定理和余弦定理分别是什么?新闻资讯11-09 -
 中位线定理的证明方法新闻资讯11-26
中位线定理的证明方法新闻资讯11-26 -
 等腰三角形面积公式是什么?已知腰长该如何求解?新闻资讯10-31
等腰三角形面积公式是什么?已知腰长该如何求解?新闻资讯10-31 -
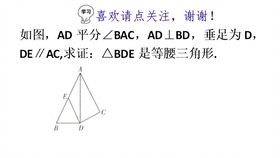 问答揭秘:如何轻松验证直角三角形斜边中线的独特定理?新闻资讯10-26
问答揭秘:如何轻松验证直角三角形斜边中线的独特定理?新闻资讯10-26 -
 切割线定理的详细证明过程新闻资讯11-23
切割线定理的详细证明过程新闻资讯11-23












