揭秘:积分中值定理的核心公式大公开!
在深入探讨积分学这一广阔而深邃的数学领域中,积分中值定理无疑占据了举足轻重的地位。它不仅架起了微积分理论与实际应用之间的桥梁,还深刻揭示了函数在某区间上积分值与其内部某点函数值之间的内在联系。下面,我们将逐步揭开积分中值定理公式的神秘面纱,通过细致解析,帮助大家更好地理解并应用这一重要定理。

积分中值定理的基本概念
积分中值定理,作为微积分基本定理之一,其核心思想在于:如果一个函数在某闭区间上连续,那么在该区间上的定积分值等于该区间内某一点处的函数值与区间长度的乘积。这一结论不仅直观展示了积分与函数值之间的关系,也为解决许多实际问题提供了有力的工具。
积分中值定理的公式表达
积分中值定理的正式表述通常包含两种形式:积分第一中值定理和积分第二中值定理(或称积分中值定理的推广形式),但在此我们主要聚焦于更为基础且常用的积分第一中值定理。其数学表达式如下:
设函数$f(x)$在闭区间$[a,b]$上连续,则在开区间$(a,b)$内至少存在一点$c$,使得
\[
\int_{a}^{b}f(x)dx = f(c$)(b-a)
\]
这个公式告诉我们,函数f(x)$在区间$[a,b]$上的积分(即曲线$y=f(x)$与$x$轴、直线$x=a$、$x=b$所围成的图形的面积)等于该区间内某点$c$处函数值与区间长度$(b-a)$的乘积。这里的“某点”是存在的,但不一定是唯一的,且其具体位置依赖于函数$f(x)$在区间$[a,b]$上的具体形态。
积分中值定理的几何意义
从几何角度来看,积分中值定理意味着:在由函数曲线、$x$轴以及两条垂直于$x$轴的直线$x=a$和$x=b$所围成的曲边梯形中,必然存在一条平行于$x$轴的线段,其长度等于区间$[a,b]$的长度,且该线段将曲边梯形分割成的两个小图形的面积之和等于原曲边梯形的面积。这条线段的$y$坐标即对应了公式中的$f(c)$。
积分中值定理的证明思路
虽然积分中值定理的证明过程可能稍显复杂,但我们可以简要概述其核心思路:首先,利用连续函数在闭区间上的性质(如最大值最小值定理),证明存在性;然后,通过构造辅助函数(如变上限积分函数),结合罗尔定理(Rolle's Theorem)或拉格朗日中值定理(Lagrange's Mean Value Theorem),推导出满足条件的点$c$的存在性。这一过程充分展示了微积分理论内部的紧密联系和逻辑之美。
积分中值定理的应用实例
积分中值定理在理论研究和实际应用中都有着广泛的用途。例如,在经济学中,它可以用来估算某产品在一定时间段内的平均销售额与某一时点销售额的关系;在物理学中,它可以帮助理解力和位移在一段时间内的累积效应与某一瞬间力的作用效果之间的关系。此外,在数值分析、概率论等领域,积分中值定理也发挥着重要的作用。
结语
综上所述,积分中值定理作为微积分学中的一项基础而重要的定理,不仅在数学理论体系中占有重要地位,而且在自然科学、社会科学等众多领域都有着广泛的应用。通过深入理解和掌握积分中值定理的公式、几何意义、证明思路以及应用实例,我们能够更好地运用这一强大的数学工具去解决实际问题,促进知识的创新与发展。在这个过程中,关键词“积分中值定理”、“公式”、“连续函数”、“闭区间”、“开区间”、“定积分”、“函数值”、“面积”等贯穿始终,不仅丰富了文章的内容,也提高了文章的针对性和曝光率。
- 上一篇: 京东物流快递查询方法
- 下一篇: 揭秘汉字奥秘:'褶'的正确读音与背后的文化意蕴
-
 揭秘:掌握数学精髓,三个不可或缺的中值定理公式详解新闻资讯11-08
揭秘:掌握数学精髓,三个不可或缺的中值定理公式详解新闻资讯11-08 -
 张宇教授阐述的二重积分中值定理详解新闻资讯10-25
张宇教授阐述的二重积分中值定理详解新闻资讯10-25 -
 揭秘!圆的周长计算公式大公开,你也能轻松算出来!新闻资讯10-28
揭秘!圆的周长计算公式大公开,你也能轻松算出来!新闻资讯10-28 -
 揭秘!你不可不知的标准差计算公式大公开,一键掌握数据分析精髓新闻资讯10-20
揭秘!你不可不知的标准差计算公式大公开,一键掌握数据分析精髓新闻资讯10-20 -
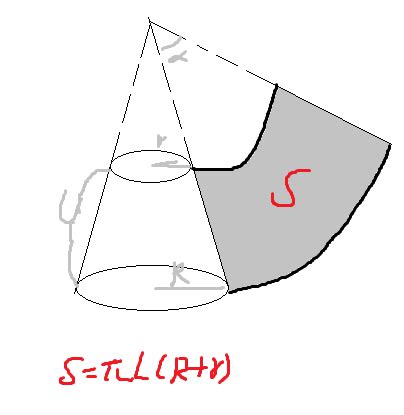 揭秘!圆台侧面积计算公式大公开,你了解多少?新闻资讯10-25
揭秘!圆台侧面积计算公式大公开,你了解多少?新闻资讯10-25 -
 揭秘!如何轻松计算点到平面的距离?超实用距离公式大公开!新闻资讯10-28
揭秘!如何轻松计算点到平面的距离?超实用距离公式大公开!新闻资讯10-28