如何计算和应用标准差公式?
在网络信息浩瀚的海洋中,标准差公式(Standard Deviation Formula)作为统计学中的一个核心概念,扮演着衡量数据离散程度的重要角色。它不仅在学术研究、科学实验、经济分析、金融风险管理等领域广泛应用,还深刻地影响着我们的日常生活决策。本文将通过解析标准差公式的含义、计算方法、应用场景以及它如何帮助我们理解和分析数据,带领读者一窥这一统计工具的奥秘。

一、标准差公式的定义与解读
标准差,简称SD(Standard Deviation),是统计学中描述数据分布离散程度的一种量化指标。它反映了数据集中各个数值与平均值之间的平均差异大小。标准差越大,说明数据点越分散,即数据的变异性或波动性较大;反之,标准差越小,则数据点越集中,数据的变异性较小。
标准差公式的基本形式为:

\[ \sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2} \]

其中,\(\sigma\) 表示标准差,\(N\) 是数据点的总数,\(x_i\) 是每一个数据点,\(\mu\) 是这些数据的平均值(Mean),\(\sum\) 表示求和运算,\(\sqrt{}\) 表示开平方运算。
这个公式告诉我们,为了计算标准差,首先需要找到数据的平均值,然后计算每个数据点与平均值的差的平方,接着对这些平方差求平均值,最后对这个平均值开平方。这个过程实质上是在测量数据分布围绕其中心(即平均值)的伸展或压缩程度。
二、标准差公式的计算步骤
1. 计算平均值:首先,需要求出数据集中所有数值的平均值。平均值是所有数值相加后除以数值的数量。
2. 计算每个数据点与平均值的差:接着,对每个数据点执行减法操作,从该数据点中减去平均值,得到一系列差值。
3. 计算差值的平方:为了消除负号并强调偏离程度,将上一步得到的每个差值平方。
4. 计算平方差的平均值:将所有平方差相加,然后除以数据点的数量(\(N\)),得到平方差的平均值。
5. 开方:最后,对上一步得到的平均值开平方,得到的结果就是标准差。
三、标准差公式的应用场景
1. 质量管理:在制造业中,标准差被用来监控产品质量的稳定性。如果产品的某个关键指标的标准差突然增大,可能意味着生产过程出现了问题,需要及时调整。
2. 金融市场分析:在投资领域,标准差是衡量投资组合风险的重要指标。较高的标准差意味着投资收益的波动性大,风险较高;而较低的标准差则表明投资收益相对稳定,风险较低。
3. 科学研究:在进行实验设计时,了解实验数据的标准差有助于评估实验结果的可靠性和可重复性。标准差较小通常意味着实验结果较为一致,科学结论更为可靠。
4. 教育评估:在教育领域,标准差可用于评估学生成绩分布的均匀性。如果标准差较大,说明学生成绩差异显著,可能需要调整教学方法或提供个性化辅导。
5. 人口统计学:在人口统计学研究中,标准差可用于分析不同群体的收入、身高、体重等指标的分布情况,揭示社会经济发展的不平衡性。
四、标准差公式的局限性与拓展
尽管标准差是一个强大的统计工具,但它也存在一定的局限性。例如,它对于极端值(即异常值)较为敏感,可能会影响整体数据分布的准确性。此外,标准差只能衡量数据分布的宽度,而不能反映数据的形状或分布的类型(如正态分布、偏态分布等)。
为了克服这些局限,统计学家们开发了多种扩展指标和方法,如变异系数(Coefficient of Variation, CV)、四分位距(Interquartile Range, IQR)等,以及更复杂的统计模型来全面分析和解释数据。
结语
标准差公式作为统计学中的基石之一,以其独特的视角和量化能力,为我们提供了一种深入理解数据分布特征的有效手段。无论是在学术探索、商业决策还是日常生活中,掌握标准差的概念和计算方法都将使我们更加科学地面对数据,做出更加明智的决策。然而,我们也应认识到其局限性,并学会结合其他统计工具和方法,以全面、准确地把握数据的本质。
-
 精准计算标准差:公式解析与应用新闻资讯10-26
精准计算标准差:公式解析与应用新闻资讯10-26 -
 数学标准差计算公式的详解新闻资讯10-25
数学标准差计算公式的详解新闻资讯10-25 -
 揭秘!你不可不知的标准差计算公式大公开,一键掌握数据分析精髓新闻资讯10-20
揭秘!你不可不知的标准差计算公式大公开,一键掌握数据分析精髓新闻资讯10-20 -
 标准差计算方法详解:轻松掌握统计分析的关键指标新闻资讯11-26
标准差计算方法详解:轻松掌握统计分析的关键指标新闻资讯11-26 -
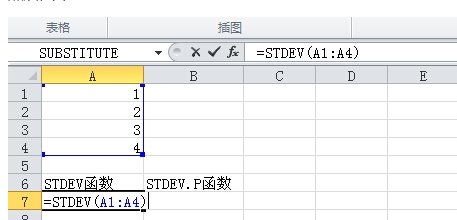
 如何在Excel中计算标准差?新闻资讯11-03
如何在Excel中计算标准差?新闻资讯11-03 -
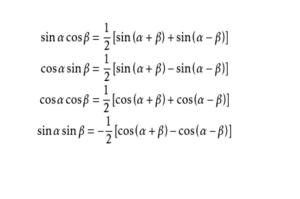 如何理解和应用积化和差公式解决数学问题?新闻资讯12-22
如何理解和应用积化和差公式解决数学问题?新闻资讯12-22