标准差计算方法详解:轻松掌握统计分析的关键指标
标准差是一种统计度量,用于量化一组数值数据的离散程度或分布宽度。当我们提到标准差时,我们通常会涉及一系列与之相关的概念和方法,如方差、均值、数据的分布类型(正态分布、偏态分布等)以及标准差在实际应用中的意义。以下是关于如何计算标准差以及与之相关的一些详细解释。
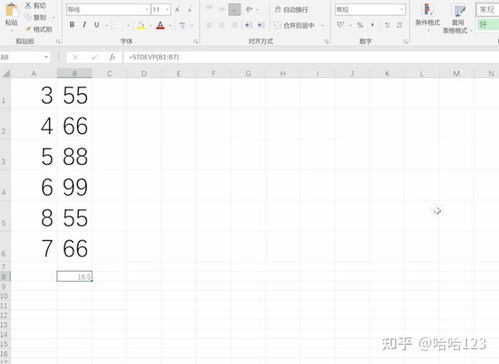
在统计学中,标准差用于测量数据集中各个数值与均值之间的偏差程度。简单来说,标准差越小,数据点越接近均值,表明数据分布比较集中;标准差越大,数据点越分散,表明数据分布比较广泛。标准差计算的基础是方差,方差是每个数据点与均值之差的平方的平均值,而标准差则是方差的平方根。

要计算标准差,首先需要确定数据集的均值。均值是所有数值的总和除以数值的数量。假设我们有一个数据集,包含n个数值x1, x2, ..., xn,均值(μ)的计算公式为:μ = (x1 + x2 + ... + xn) / n。

一旦确定了均值,就可以计算每个数据点与均值之间的偏差。偏差是每个数据点减去均值的结果,表示为:dx = xi - μ,其中xi是数据集中的每个数值。
接下来,计算每个偏差的平方,然后求这些平方值的平均值,这个平均值就是方差(σ²)。方差计算公式为:σ² = Σ(dx²) / n,其中Σ表示求和,dx²是每个偏差的平方,n是数据点的数量。方差提供了数据点与均值之间偏差大小的度量,但它使用了平方值,因此单位是原始数据单位的平方。
为了回到与原始数据相同的单位,并得到一个更直观的度量,我们计算方差的平方根,即标准差(σ)。标准差计算公式为:σ = √(σ²),它将方差转换回与原始数据相同的单位,使得我们可以更容易地解释数据的离散程度。
值得注意的是,标准差的计算还可以根据数据的具体情况进行调整。如果数据集包含大量的数据点,且我们希望获得更稳定的估计,可以使用样本标准差公式,而不是总体标准差公式。样本标准差在计算方差时使用的是n-1作为分母(而不是n),这被称为贝塞尔修正,它有助于更好地估计从总体中随机抽取的样本的方差。样本标准差公式为:s = √[Σ(dx²) / (n-1)]。
除了基本的概念和计算,标准差还有一些重要的性质和解释。首先,标准差是度量数据离散程度的一个指标,但它并不是唯一的指标。其他常用的离散程度度量包括极差(最大值与最小值之差)、四分位数间距(第一四分位数与第三四分位数之差)等。然而,标准差具有一些独特的优势,比如它对所有数据点都赋予了权重(通过平方操作),这使得它对极端值(异常值)更为敏感。
标准差的另一个重要性质是它与正态分布的关系。正态分布是一种重要的连续概率分布,它的形状由均值和标准差决定。在正态分布中,标准差决定了数据分布的宽度或分散程度。具体来说,大约68%的数据点位于均值的一个标准差范围内,95%的数据点位于均值的两个标准差范围内,99.7%的数据点位于均值的三个标准差范围内。这些比例关系使得我们可以使用标准差来估计数据点落在某个范围内的概率。
标准差在实际应用中具有广泛的意义。例如,在金融领域,标准差常用于衡量股票或投资组合的波动性。较高的标准差意味着价格波动较大,可能带来更高的风险;较低的标准差则意味着价格波动较小,可能带来更低的风险。在质量管理中,标准差用于评估产品质量的稳定性和一致性。较小的标准差表明产品质量更加稳定,更容易满足客户的需求和期望。
此外,标准差还在其他许多领域发挥着重要作用。在生物学中,标准差用于衡量实验数据的变异性;在教育学中,标准差用于评估学生的成绩分布;在市场调研中,标准差用于分析消费者偏好和行为的差异性。无论在哪个领域,标准差都提供了一种量化数据离散程度的有效方法,有助于我们更好地理解数据的分布特征和潜在规律。
最后,需要指出的是,虽然标准差是一种强大的统计工具,但它也有一些局限性。例如,当数据存在极端值时,标准差可能会受到较大影响,导致对数据离散程度的估计不准确。此外,标准差对数据的对称性比较敏感,如果数据分布严重偏斜,那么标准差可能无法很好地反映数据的真实离散程度。因此,在使用标准差时,我们需要结合数据的具体情况和其他统计指标进行综合分析,以获得更全面和准确的结论。
总的来说,标准差是一种重要的统计度量,它提供了量化数据离散程度的有效方法。通过计算标准差,我们可以更好地理解数据的分布特征和潜在规律,为决策提供科学依据。然而,我们也需要注意到标准差的局限性和适用范围,在实际应用中结合其他统计指标进行综合分析。
- 上一篇: 探寻清明节的传统习俗魅力
- 下一篇: 兴业银行客服电话是多少?
-
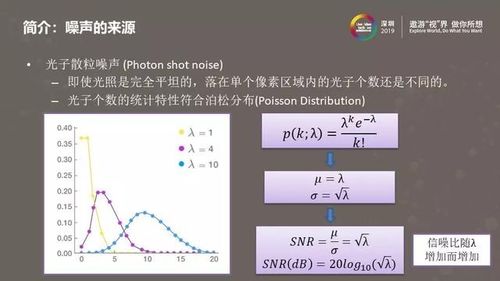 数学标准差计算公式的详解新闻资讯10-25
数学标准差计算公式的详解新闻资讯10-25 -
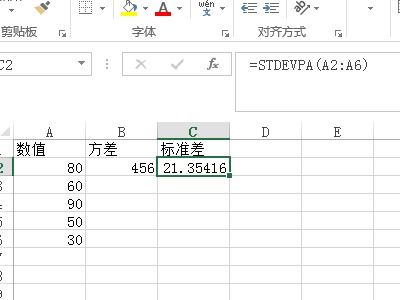 如何在Excel中计算标准差?新闻资讯11-03
如何在Excel中计算标准差?新闻资讯11-03 -
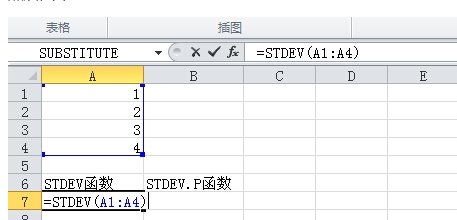 揭秘!你不可不知的标准差计算公式大公开,一键掌握数据分析精髓新闻资讯10-20
揭秘!你不可不知的标准差计算公式大公开,一键掌握数据分析精髓新闻资讯10-20 -
 如何计算和应用标准差公式?新闻资讯12-22
如何计算和应用标准差公式?新闻资讯12-22 -
 精准计算标准差:公式解析与应用新闻资讯10-26
精准计算标准差:公式解析与应用新闻资讯10-26 -
 揭秘毛利率计算的奥秘:轻松掌握盈利关键指标新闻资讯10-19
揭秘毛利率计算的奥秘:轻松掌握盈利关键指标新闻资讯10-19










