精准计算标准差:公式解析与应用
在探讨数据分析与统计学的广阔领域中,标准差(Standard Deviation)无疑是一个核心概念,它为我们提供了一种量化数据分散程度的方法。标准差不仅在数学、统计学中占据重要地位,还在经济学、金融学、生物学、心理学等多个学科中发挥着关键作用。本文旨在深入浅出地介绍标准差公式的由来、计算方法、意义及应用,帮助读者全面理解这一统计工具。

一、标准差的概念起源
标准差的概念最早可以追溯到17世纪,由数学家卡尔·弗里德里希·高斯(Carl Friedrich Gauss)在其对误差分布理论的研究中明确提出。高斯发现,许多自然现象和实验误差的分布都遵循一种特定的曲线——正态分布(高斯分布),而标准差正是描述这种分布形态宽度(即数据离散程度)的关键参数。

二、标准差公式的定义
标准差是衡量数据集中各个数值与平均值之间差异大小的统计量。其计算公式基于每个数据点与平均值的差的平方的平均值的平方根。具体地,对于一组数据$X = \{x_1, x_2, ..., x_n\}$,其标准差$\sigma$的计算步骤如下:
1. 计算平均值:首先,计算数据的算术平均值(均值)$\mu$,公式为

\[
\mu = \frac{1}{n} \sum_{i=1}^{n} x_i
\]
其中,$n$是数据的数量。
2. 计算每个数据点与平均值的差:接着,对于每个数据点$x_i$,计算其与平均值$\mu$的差,即$x_i - \mu$。
3. 计算差的平方:将上述差值平方,得到$(x_i - \mu)^2$。这一步是为了消除正负差值的相互抵消效应,确保所有偏差都被正向考虑。
4. 计算平方差的平均值:将所有平方差相加后除以数据点的数量$n$(或有时为了得到样本标准差而使用$n-1$作为除数,这取决于数据是总体还是样本),得到方差$s^2$(或$\sigma^2$,对于总体):
\[
s^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2 \quad \text{(样本方差)}
\]
\[
\sigma^2 = \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2 \quad \text{(总体方差,} N \text{为总体大小)}
\]
5. 求平方根得到标准差:最后,对方差取平方根,即得到标准差$\sigma$(或样本标准差$s$):
\[
\sigma = \sqrt{\sigma^2} = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2} \quad \text{(总体标准差)}
\]
\[
s = \sqrt{s^2} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2} \quad \text{(样本标准差)}
\]
三、标准差的意义
标准差是衡量数据波动性的重要指标。一个较大的标准差意味着数据点分布得更加分散,即数据中存在较大的差异;相反,较小的标准差则表明数据点较为集中,差异较小。标准差不仅能够帮助我们了解数据的离散程度,还能在数据分析、质量控制、风险评估等多个领域发挥重要作用。
四、标准差的应用
1. 数据分析:在数据分析中,标准差常用于识别异常值(即远离平均值的极端数据点),这些异常值可能对整体分析结果产生显著影响。
2. 质量控制:在制造业中,标准差被广泛应用于质量控制过程,如六西格玛管理中,通过减少过程变异(即降低标准差),来提高产品质量和顾客满意度。
3. 风险评估:在金融领域,标准差是衡量投资组合风险的关键指标之一。通过计算投资组合中各资产的标准差及它们之间的协方差,可以评估整个投资组合的风险水平。
4. 社会科学研究:在心理学、教育学等社会科学领域,标准差用于量化不同群体之间的差异,帮助研究者理解不同变量之间的关系。
五、结语
标准差作为统计学中的一个基础而强大的工具,其重要性不言而喻。通过本文的介绍,我们了解了标准差公式的由来、计算方法、意义以及广泛的应用领域。掌握标准差不仅能够帮助我们更深入地理解数据的本质特征,还能在多个领域中指导我们做出更加科学、合理的决策。希望读者能够从中受益,并在未来的学习和工作中灵活运用这一统计工具。
- 上一篇: 一秒直达!如何超快速切换回电脑桌面的神奇技巧
- 下一篇: 一问一答揭秘:忘记的英文怎么说?
-
 如何计算和应用标准差公式?新闻资讯12-22
如何计算和应用标准差公式?新闻资讯12-22 -
 数学标准差计算公式的详解新闻资讯10-25
数学标准差计算公式的详解新闻资讯10-25 -
 揭秘!你不可不知的标准差计算公式大公开,一键掌握数据分析精髓新闻资讯10-20
揭秘!你不可不知的标准差计算公式大公开,一键掌握数据分析精髓新闻资讯10-20 -
 精准掌握:相对偏差计算公式的深度解析新闻资讯11-17
精准掌握:相对偏差计算公式的深度解析新闻资讯11-17 -
 标准差计算方法详解:轻松掌握统计分析的关键指标新闻资讯11-26
标准差计算方法详解:轻松掌握统计分析的关键指标新闻资讯11-26 -
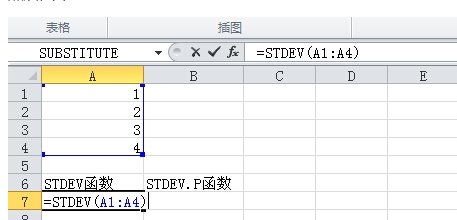
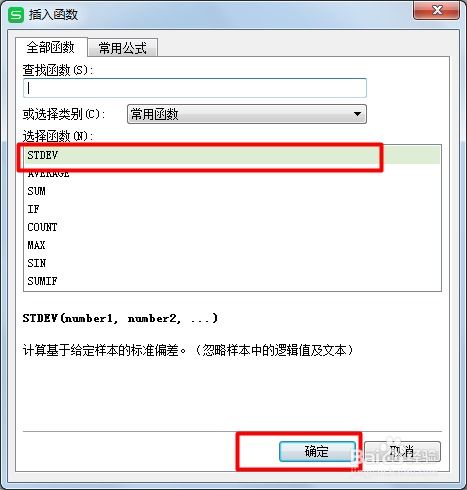
 如何在Excel中计算标准差?新闻资讯11-03
如何在Excel中计算标准差?新闻资讯11-03