线性代数基础:范德蒙德行列式详解与计算方法
线性代数作为数学的一个重要分支,广泛应用于计算机科学、物理学、工程学等多个领域。其中,范德蒙德行列式(Vandermonde Determinant)作为线性代数中的一个重要概念,具有独特的性质和广泛的应用。本文旨在介绍范德蒙德行列式的定义、性质及其计算方法,并通过实例加深理解。

范德蒙德行列式起源于范德蒙德矩阵,它是一种特殊的方阵,其特点在于每一行的元素构成等比数列或等差数列的某种变形。具体来说,对于一个n阶范德蒙德矩阵V,其第i行第j列的元素v_{ij}为某个基数a_{i}的j-1次幂,即v_{ij} = a_{i}^{j-1}。

首先,我们来看范德蒙德行列式的定义。对于一个n阶范德蒙德矩阵V,其行列式称为范德蒙德行列式,记作D_{n} = det(V)。范德蒙德行列式在形式上非常简洁,但在计算上却具有相当的复杂性。其重要性在于,范德蒙德行列式不为零(即V是可逆矩阵)当且仅当矩阵V的各行基数a_{i}互不相同。这一性质使得范德蒙德行列式在多项式插值、信号处理等领域有着广泛的应用。

接下来,我们探讨范德蒙德行列式的计算方法。直接通过行列式的展开式来计算范德蒙德行列式是相当复杂的,因为需要计算n!项。然而,通过归纳法和一些数学技巧,我们可以得到范德蒙德行列式的显式公式。

设n阶范德蒙德矩阵V的基数为a_{1}, a_{2}, ..., a_{n},则范德蒙德行列式D_{n}可以表示为:
D_{n} = ∏_{1≤i
这个公式看起来有些复杂,但实际上却非常直观。它表示所有可能的基数对(a_{i}, a_{j})(i < j)之差的乘积。这个公式的推导过程涉及归纳法和行列式的性质,虽然在这里不详细展开,但我们可以通过这个公式快速计算范德蒙德行列式的值。
为了加深理解,我们来看一个具体的例子。设三阶范德蒙德矩阵V的基数为1, 2, 3,则:
V = [
[1, 1, 1],
[1, 2, 4],
[1, 3, 9]
根据范德蒙德行列式的公式,我们有:
D_{3} = (2-1)(3-1)(3-2) × (3-1)(2-1) = 1×2×1 × 2×1 = 4
这个计算结果与直接通过行列式展开式计算得到的结果是一致的。
范德蒙德行列式的性质使得它在许多数学问题中发挥着重要作用。例如,在多项式插值问题中,给定一组不同的x值和对应的y值,我们可以构造一个多项式通过这些点。范德蒙德行列式在这个问题中起着关键作用,因为它可以帮助我们确定多项式的系数。具体来说,如果我们设多项式的系数为c_{i},则这些系数可以通过解一个以范德蒙德矩阵为系数矩阵的线性方程组得到。
此外,范德蒙德行列式还在信号处理、编码理论等领域有着广泛的应用。例如,在循环码(Cyclic Codes)的构造中,范德蒙德行列式被用来确定码字的线性独立性。在信号处理中,范德蒙德矩阵的逆矩阵可以用来对信号进行滤波和重构。
值得注意的是,虽然范德蒙德行列式具有许多重要的性质和广泛的应用,但它的计算复杂度也是相当高的。特别是当n很大时,计算范德蒙德行列式需要消耗大量的时间和资源。因此,在实际应用中,我们通常需要寻找一些有效的算法来加速计算过程。例如,通过利用范德蒙德行列式的递归性质和快速傅里叶变换(FFT)等技术,我们可以大大降低计算复杂度。
除了范德蒙德行列式本身外,范德蒙德矩阵还具有一些其他有趣的性质和应用。例如,范德蒙德矩阵是一个完全可分解矩阵(Totally Decomposable Matrix),这意味着它的特征多项式可以表示为一系列一次多项式的乘积。这个性质使得范德蒙德矩阵在特征值计算和矩阵分解等问题中具有重要的应用价值。
此外,范德蒙德矩阵还与一些著名的数学问题紧密相关。例如,范德蒙德矩阵的逆矩阵与拉格朗日插值多项式(Lagrange Interpolation Polynomial)的系数之间存在直接关系。这个关系使得范德蒙德矩阵在多项式插值和数值分析中发挥着重要作用。
综上所述,范德蒙德行列式是线性代数中一个重要的概念,具有独特的性质和广泛的应用。通过深入了解范德蒙德行列式的定义、计算方法和应用,我们可以更好地理解和应用线性代数知识,为解决实际问题提供有力的数学工具。同时,我们也需要注意到范德蒙德行列式计算复杂度高的问题,并尝试寻找有效的算法来加速计算过程。在未来的研究中,我们可以进一步探索范德蒙德行列式在其他领域的应用潜力,以及如何通过优化算法来提高计算效率。
- 上一篇: 如何在百度云上打开BT种子文件?
- 下一篇: 家常羊杂汤的简易制作方法
-
 揭秘范德蒙德行列式:定义与形式详解新闻资讯11-04
揭秘范德蒙德行列式:定义与形式详解新闻资讯11-04 -
 投影向量的具体计算公式详解新闻资讯10-22
投影向量的具体计算公式详解新闻资讯10-22 -
 矩阵乘法的定义与运算方法新闻资讯11-22
矩阵乘法的定义与运算方法新闻资讯11-22 -
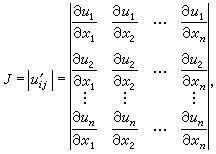 雅可比行列式详解新闻资讯11-05
雅可比行列式详解新闻资讯11-05 -
 轻松掌握行列区分技巧,提升数据处理效率新闻资讯10-24
轻松掌握行列区分技巧,提升数据处理效率新闻资讯10-24 -
 揭秘矩阵乘法:解锁线性代数的核心运算新闻资讯11-17
揭秘矩阵乘法:解锁线性代数的核心运算新闻资讯11-17