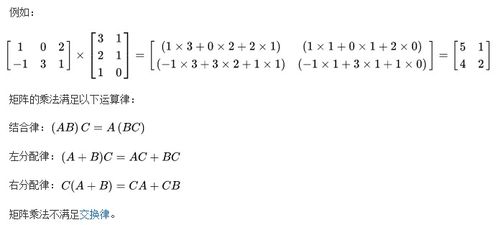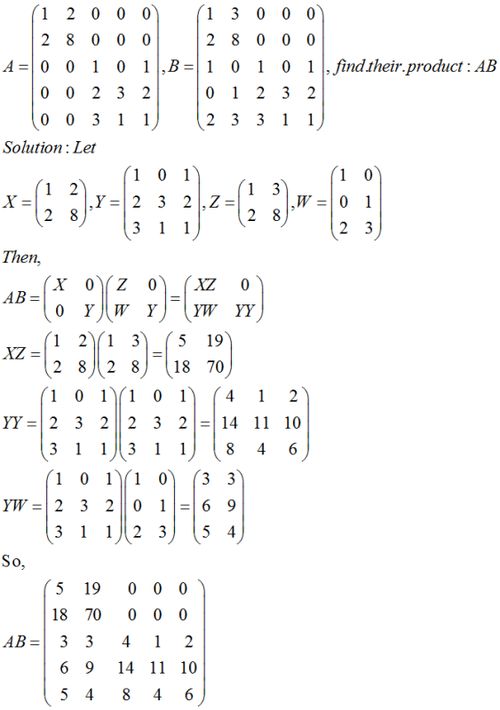矩阵乘法的定义与运算方法
矩阵的乘法运算详解

矩阵的乘法运算是一种线性代数中的重要运算,广泛应用于计算机图形学、物理学、工程学以及经济学等多个领域。理解并掌握矩阵乘法不仅能够帮助我们解决复杂的线性方程组,还能在计算和优化问题中发挥重要作用。下面,我们将详细解析矩阵乘法的定义、步骤、性质以及一些实际的应用案例。
一、矩阵乘法的定义
矩阵乘法有两种类型:标量乘法和矩阵乘法(也称为线性变换或矩阵乘积)。标量乘法是指一个矩阵与一个标量(实数或复数)相乘,结果是一个与原矩阵同形状的矩阵,其中每个元素都是原矩阵对应元素与标量的乘积。
我们重点讨论的是矩阵乘法,即两个矩阵相乘。假设我们有两个矩阵A和B,A是一个m×n矩阵,B是一个n×p矩阵,那么它们的乘积C=AB是一个m×p矩阵。矩阵C中的元素c_ij是A的第i行与B的第j列对应元素乘积的和。
二、矩阵乘法的步骤
1. 确定矩阵可乘性:
在进行矩阵乘法之前,首先要确定两个矩阵是否可以相乘。具体来说,假设A是一个m×n矩阵,B是一个n×p矩阵,只有当A的列数等于B的行数(即n=n')时,矩阵A和B才能相乘。
2. 计算乘积矩阵的元素:
设C=AB,则C是一个m×p矩阵。矩阵C中的元素c_ij由以下公式计算:
c_ij = Σ (a_ik * b_kj) (其中k从1到n)
也就是说,c_ij等于A的第i行与B的第j列对应元素乘积的和。
3. 构造乘积矩阵:
通过计算所有c_ij的值,我们可以构造出乘积矩阵C。
三、矩阵乘法的性质
1. 不满足交换律:
一般来说,矩阵乘法不满足交换律,即AB不一定等于BA。只有当矩阵A和B满足特定条件(如A和B都是方阵且其中一个矩阵是可逆矩阵时),乘积才可能相等。
2. 满足结合律和分配律:
矩阵乘法满足结合律,即(AB)C=A(BC);同时,它也满足分配律,即A(B+C)=AB+AC和(A+B)C=AC+BC。
3. 单位矩阵:
任何矩阵与单位矩阵相乘都等于它本身。单位矩阵是一个方阵,其对角线上的元素都是1,其余元素都是0。
4. 零矩阵:
任何矩阵与零矩阵相乘都等于零矩阵。零矩阵是一个所有元素都是0的矩阵。
四、矩阵乘法的实际应用
1. 线性方程组:
矩阵乘法可以用于求解线性方程组。通过将线性方程组的系数和常数项表示为矩阵形式,我们可以利用矩阵乘法求解未知数。
2. 图像处理:
在计算机图形学中,矩阵乘法被广泛应用于图像的变换(如旋转、缩放和平移)中。通过矩阵运算,我们可以对图像进行各种复杂的变换操作。
3. 机器学习:
在机器学习中,矩阵乘法是神经网络、支持向量机和线性回归等算法的基础。通过矩阵运算,我们可以高效地计算梯度、更新权重并优化模型性能。
4. 经济学:
在经济学中,矩阵乘法被用于计算投入产出表、预测经济趋势以及优化资源配置等问题。通过构建矩阵模型,我们可以更好地理解和预测经济系统的行为。
五、矩阵乘法的实例
假设我们有两个矩阵A和B:
A = [1, 2; 3, 4]
B = [5, 6; 7, 8]
我们需要计算它们的乘积C=AB。
首先,我们确认A和B可以相乘(因为A的列数等于B的行数)。
然后,我们计算C的每个元素:
c_11 = 1*5 + 2*7 = 5 + 14 = 19
c_12 = 1*6 + 2*8 = 6 + 16 = 22
c_21 = 3*5 + 4*7 = 15 + 28 = 43
c_22 = 3*6 + 4*8 = 18 + 32 = 50
因此,乘积矩阵C为:
C = [19, 22; 43, 50]
六、总结
矩阵乘法是线性代数中的基础运算之一,具有广泛的应用价值。通过掌握矩阵乘法的定义、步骤和性质,我们可以更好地理解和应用这一运算。同时,通过实际案例的演练,我们可以加深对矩阵乘法的理解和掌握程度。无论是在科学研究还是工程应用中,矩阵乘法都发挥着不可替代的作用。因此,我们应该重视这一运算的学习和实践,不断提高自己的数学素养和解决实际问题的能力。
- 上一篇: 如何查询中国邮政挂号信的状态?
- 下一篇: 揭秘“IC”背后的含义:全面了解这个缩写代表什么
-
 矩阵的乘法运算是怎么进行的?新闻资讯11-17
矩阵的乘法运算是怎么进行的?新闻资讯11-17 -
 揭秘矩阵乘法:解锁线性代数的核心运算新闻资讯11-17
揭秘矩阵乘法:解锁线性代数的核心运算新闻资讯11-17 -
 揭秘:矩阵乘法运算的详细步骤新闻资讯12-13
揭秘:矩阵乘法运算的详细步骤新闻资讯12-13 -
 Excel中乘法的多样高效计算方法新闻资讯11-04
Excel中乘法的多样高效计算方法新闻资讯11-04 -
 Excel中乘法运算的轻松掌握:让你的数据计算飞起来!新闻资讯10-29
Excel中乘法运算的轻松掌握:让你的数据计算飞起来!新闻资讯10-29 -
 如何有效教孩子记忆九九乘法口诀表?新闻资讯11-22
如何有效教孩子记忆九九乘法口诀表?新闻资讯11-22