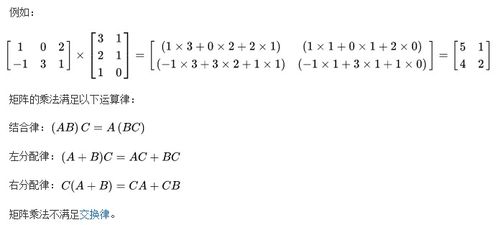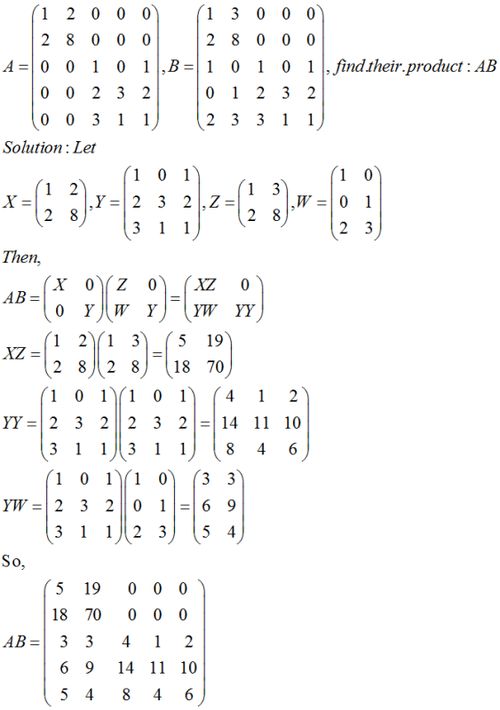揭秘矩阵乘法:解锁线性代数的核心运算
矩阵的乘法运算是线性代数中一个极其重要的概念,它在科学计算、工程技术、计算机科学以及经济学等多个领域都有广泛的应用。为了更好地理解这一概念,我们首先需要明确矩阵的基本概念,进而深入探讨矩阵乘法的定义、性质以及具体计算方法。

矩阵是一个矩形数组,由行和列组成,其中的元素可以是实数、复数或者其他数学对象。一个m行n列的矩阵通常记作A_{m×n},或简称为A。矩阵中的元素用a_{ij}表示,其中i表示行号,j表示列号。例如,一个2行3列的矩阵A可以表示为:

A = [a_{11} a_{12} a_{13}
a_{21} a_{22} a_{23}]
矩阵乘法是一种线性代数运算,涉及两个矩阵的乘积。给定两个矩阵A和B,其中A是m行n列的矩阵,B是n行p列的矩阵,那么它们的乘积C是一个m行p列的矩阵,记作C = AB。矩阵乘法的定义要求A的列数必须与B的行数相等,这是乘法运算能够进行的前提条件。
矩阵C中的元素c_{ij}是通过取A的第i行与B的第j列对应元素相乘后求和得到的。具体地,c_{ij}的计算公式为:
c_{ij} = Σ(a_{ik} * b_{kj}),其中k从1到n
这个求和过程实际上是对A的第i行与B的第j列的点积运算。
为了更好地理解矩阵乘法,我们来看一个具体的例子。假设有两个矩阵A和B:
A = [1 2
3 4]
B = [5 6
7 8]
我们要计算它们的乘积C = AB。根据矩阵乘法的定义,我们有:
c_{11} = 1*5 + 2*7 = 5 + 14 = 19
c_{12} = 1*6 + 2*8 = 6 + 16 = 22
c_{21} = 3*5 + 4*7 = 15 + 28 = 43
c_{22} = 3*6 + 4*8 = 18 + 32 = 50
因此,矩阵C为:
C = [19 22
43 50]
矩阵乘法满足一些重要的性质,这些性质对于理解和应用矩阵乘法至关重要。首先,矩阵乘法不满足交换律,即AB不一定等于BA。但是,矩阵乘法满足结合律和分配律。结合律意味着(AB)C = A(BC),分配律则意味着A(B + C) = AB + AC和(A + B)C = AC + BC。
此外,矩阵乘法还有单位元和零元的概念。对于任何n阶方阵A,存在一个n阶单位矩阵I,使得AI = IA = A。单位矩阵I的对角线元素都是1,其余元素都是0。同时,存在一个零矩阵O,对于任何矩阵A,都有AO = OA = O。零矩阵的所有元素都是0。
在实际应用中,矩阵乘法常常用于解决线性方程组、变换向量和坐标、计算特征值和特征向量等问题。例如,在图像处理中,矩阵乘法可以用于图像的旋转、缩放和平移等操作。在机器学习中,矩阵乘法是神经网络前向传播和反向传播算法的基础。
矩阵乘法还与行列式、逆矩阵和矩阵的秩等概念密切相关。行列式是一个标量值,它描述了矩阵的某些几何性质,如体积、面积等。逆矩阵是一个重要的概念,它允许我们通过矩阵乘法来“撤销”另一个矩阵的作用。不是所有的矩阵都有逆矩阵,只有方阵且行列式不为0的矩阵才有逆矩阵。矩阵的秩是矩阵的一个基本属性,它表示矩阵中最大的非零子式的阶数,与矩阵的线性无关行(或列)的个数相等。
在计算矩阵乘法时,需要注意计算复杂度和优化方法。对于两个n阶方阵A和B,它们的乘积C = AB的计算复杂度是O(n^3),因为需要计算n^2个元素,每个元素需要n次乘法和n-1次加法。因此,对于大型矩阵,直接计算乘法可能会非常耗时。为了优化计算效率,人们开发了多种算法和技巧,如Strassen算法、Coppersmith-Winograd算法以及并行计算等。
此外,矩阵乘法还与向量空间、线性变换和矩阵代数等概念紧密相连。向量空间是一个包含向量和标量运算的集合,而线性变换则是向量空间中的一种特殊映射,它保持向量的加法和数乘运算不变。矩阵代数则是一套处理矩阵运算的规则和方法,包括矩阵的加法、减法、乘法、转置、逆运算等。
在经济学和金融学中,矩阵乘法也被广泛应用。例如,在投资组合优化中,可以使用矩阵乘法来计算资产的预期收益率和风险。在计量经济学中,矩阵乘法可以用于估计线性回归模型的参数。在金融工程中,矩阵乘法可以用于计算金融衍生品的定价和风险管理。
总之,矩阵的乘法运算是线性代数中的一个核心概念,它具有广泛的应用和重要的性质。通过深入理解和熟练掌握矩阵乘法的定义、计算方法和性质,我们可以更好地应用矩阵乘法来解决实际问题,提高计算效率和准确性。无论是在科学研究、工程技术还是经济金融领域,矩阵乘法都发挥着不可替代的作用。
- 上一篇: 打造吸睛海报的绝妙技巧
- 下一篇: 轻松学会水煮梨的制作方法!
-
 矩阵的乘法运算是怎么进行的?新闻资讯11-17
矩阵的乘法运算是怎么进行的?新闻资讯11-17 -
 矩阵乘法的定义与运算方法新闻资讯11-22
矩阵乘法的定义与运算方法新闻资讯11-22 -
 揭秘:矩阵乘法运算的详细步骤新闻资讯12-13
揭秘:矩阵乘法运算的详细步骤新闻资讯12-13 -
 揭秘正交矩阵:四大精妙判定法,轻松解锁矩阵世界奥秘新闻资讯10-30
揭秘正交矩阵:四大精妙判定法,轻松解锁矩阵世界奥秘新闻资讯10-30 -
 揭秘正交矩阵:线性代数中的神秘变换大师新闻资讯11-01
揭秘正交矩阵:线性代数中的神秘变换大师新闻资讯11-01 -
 如何轻松求解矩阵的逆?新闻资讯11-08
如何轻松求解矩阵的逆?新闻资讯11-08