常用反导数与积分公式
在探讨常见的反导公式时,我们不可避免地要深入理解导弹防御系统的核心机制。这类系统通常依赖于高精度的探测、跟踪、拦截以及复杂的数学计算,以确保能够有效摧毁来袭的敌方导弹。以下是对几种关键反导公式及其应用的详细阐述。

首先,我们要讨论的是导弹拦截中的关键参数之一——导弹的飞行时间。这个时间由导弹的飞行距离D、导弹的飞行速度V以及导弹的加速度a共同决定。飞行时间T的公式可以表示为:T = sqrt((2D)/(a + sqrt(V^2 + 4aD)))。这个公式不仅考虑了导弹的初始速度和加速度,还融入了导弹在飞行过程中的动能变化,从而能更准确地预测导弹到达目标的时间。
接下来,我们关注导弹的弹道轨迹,这通常由导弹的发射角度θ和初速度V0决定。弹道高度h的公式可以表示为:h = (V0^2 * sin^2(θ))/(2g)。这个公式揭示了导弹发射角度和初速度对弹道高度的直接影响,是设计导弹飞行轨迹的重要参考。同时,我们也可以利用这个公式来计算导弹在不同飞行阶段的位置,从而更精确地规划拦截策略。
在导弹防御系统中,雷达的探测距离是一个至关重要的参数。雷达探测距离R的公式为:R = sqrt((Pt * Gt * Gr * λ^2 * σ) / (64 * π^3 * N * L * kT * B * F^2))。其中,Pt是雷达发射功率,Gt是发射天线增益,Gr是接收天线增益,λ是雷达波长,σ是目标截获面积,N是噪声系数,L是系统损耗,kT是玻尔兹曼常数,B是雷达带宽,F是雷达波束形状因子。这个公式综合了雷达系统的多个关键参数,能够准确地评估雷达的探测能力,对于制定反导策略具有重要意义。
除了雷达探测距离外,导弹的命中精度也是衡量反导系统性能的重要指标。导弹的命中精度通常受到导弹飞行过程中的多种因素影响,包括空气阻力、地球引力、导弹姿态控制等。为了提高命中精度,我们通常会采用一些先进的制导算法和导航设备。这些算法和设备能够实时地测量导弹的飞行参数,并根据这些参数调整导弹的飞行轨迹。其中,导弹的落点偏差Δx和Δy的公式可以表示为:Δx = ΔV * cos(θ) * T,Δy = ΔV * sin(θ) * T - 0.5 * g * T^2。这个公式揭示了导弹速度偏差ΔV、发射角度θ以及飞行时间T对导弹落点精度的影响,为优化导弹制导算法提供了理论基础。
此外,在反导系统中,我们还需要考虑导弹的拦截效率。拦截效率通常取决于拦截弹的发射数量、发射时机以及拦截弹的性能。为了评估拦截效率,我们可以采用一些统计方法,如泊松分布、二项分布等。这些统计方法能够帮助我们预测在不同情况下拦截弹的成功率,从而优化拦截策略。
在实际应用中,反导系统还需要考虑多种复杂因素,如导弹的机动性、电磁干扰、天气条件等。这些因素都可能对导弹的飞行轨迹和命中精度产生严重影响。因此,在设计和优化反导系统时,我们需要综合考虑多种因素,并采用先进的仿真和测试技术来验证系统的性能。
为了提高反导系统的拦截能力,我们还可以采用一些先进的战术和技术手段。例如,我们可以利用多层次的防御体系来分散来袭导弹的注意力,降低单一防御单元的压力。同时,我们还可以采用分布式雷达网络和先进的通信技术来提高系统的探测和跟踪能力。此外,利用人工智能技术来优化拦截策略和提高导弹的自主作战能力也是当前研究的热点方向。
在具体实施反导任务时,我们还需要考虑导弹的发射点和拦截点的选择。这些选择将直接影响导弹的飞行轨迹和拦截效率。因此,在制定反导计划时,我们需要充分利用地形地貌、气象条件等自然因素来优化发射点和拦截点的布局。同时,我们还需要考虑导弹的发射角度和速度等参数对飞行轨迹的影响,以确保导弹能够准确地击中目标。
另外,反导系统还需要具备高度的可靠性和稳定性。这要求我们在设计和制造过程中采用高质量的材料和先进的工艺技术来确保系统的性能稳定可靠。同时,我们还需要建立完善的维护和保养体系来确保系统的长期稳定运行。
在应对不同类型的导弹威胁时,我们还需要采用不同的反导策略和手段。例如,对于高速飞行的弹道导弹,我们可以采用高空拦截的方式来降低导弹的动能和机动性;对于低空飞行的巡航导弹,我们可以采用地面拦截或舰载拦截的方式来提高拦截效率。此外,我们还可以利用电子干扰和隐身技术等手段来降低敌方导弹的探测和打击能力。
综上所述,常见的反导公式在导弹防御系统中发挥着至关重要的作用。它们不仅帮助我们准确地预测导弹的飞行轨迹和命中精度,还为我们提供了优化拦截策略和提高系统性能的理论依据。在未来的发展中,我们将继续探索和研究更加先进的反导技术和手段,以应对日益复杂的导弹威胁和挑战。
- 上一篇: 行吟诗人与吟游诗人(gleeman)有何不同?
- 下一篇: 如何查找百度健康中的我的订单
-
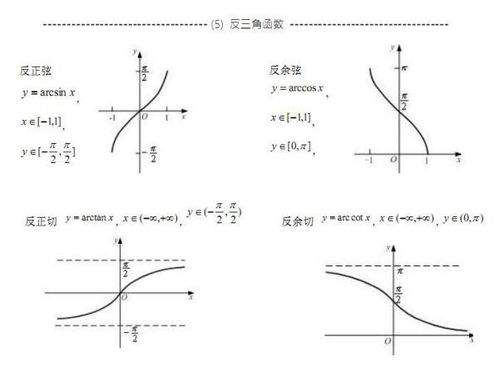 arc三角函数的导数分别是什么?新闻资讯11-22
arc三角函数的导数分别是什么?新闻资讯11-22 -
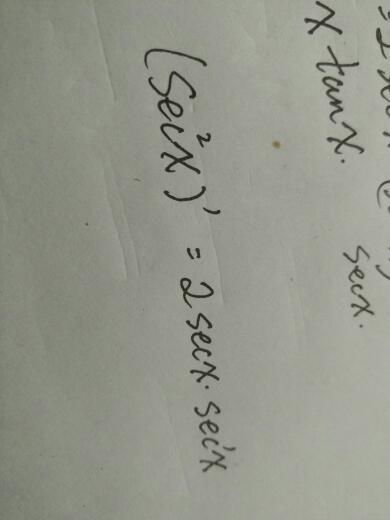 揭秘!secx的导数究竟是什么?新闻资讯10-27
揭秘!secx的导数究竟是什么?新闻资讯10-27 -
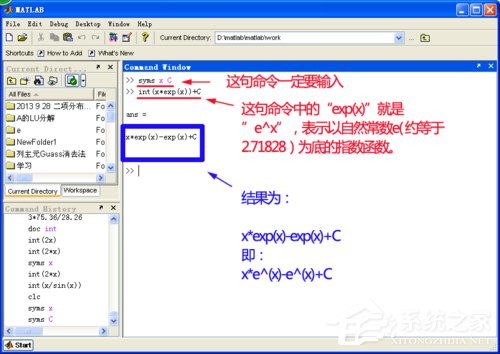 MATLAB中如何计算积分新闻资讯12-12
MATLAB中如何计算积分新闻资讯12-12 -
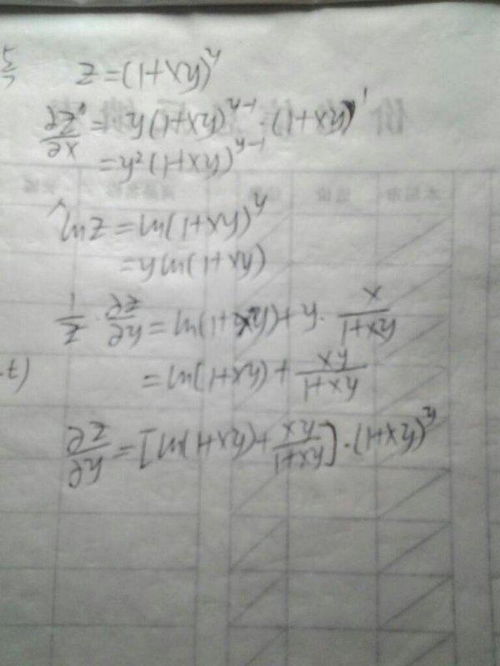 如何求解偏导数?新闻资讯11-23
如何求解偏导数?新闻资讯11-23 -
 分数求导的奥秘与技巧新闻资讯11-05
分数求导的奥秘与技巧新闻资讯11-05 -
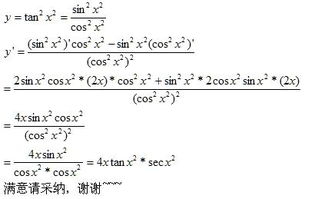 tan x 的导数是多少?如何求导?新闻资讯12-22
tan x 的导数是多少?如何求导?新闻资讯12-22