MATLAB中如何计算积分

在数值计算和工程应用中，MATLAB是一款功能强大的工具，特别适用于求解各种数学问题，包括积分。积分是数学中的一个基本概念，广泛应用于物理、工程、经济等多个领域。本文将详细介绍在MATLAB中如何求解积分，包括定积分和不定积分，以及一些常见的技巧和示例。

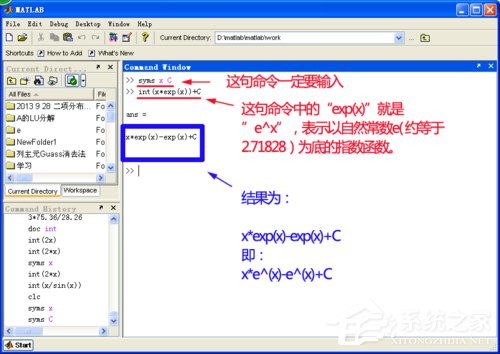
首先，我们需要明确两种积分类型：不定积分和定积分。不定积分是求一个函数的原函数或反导数，通常表示为∫f(x)dx。而定积分则是在某一区间上对函数进行积分，表示为∫[a,b]f(x)dx，其结果是一个具体的数值。

一、求解不定积分

在MATLAB中，求解不定积分主要使用`int`函数。`int`函数的基本语法是`int(f, x)`，其中`f`是需要积分的函数，`x`是积分变量。

示例1：求解简单函数的不定积分

假设我们需要求解函数f(x) = x^2的不定积分。

```matlab

syms x; % 定义符号变量

f = x^2; % 定义函数

F = int(f, x); % 求解不定积分

disp(F); % 显示结果

```

运行这段代码后，MATLAB将输出：

```

(x^3)/3

```

这表明f(x) = x^2的不定积分为F(x) = (x^3)/3。

示例2：求解复合函数的不定积分

对于更复杂的函数，如f(x) = sin(x) * cos(x)，我们也可以同样使用`int`函数求解。

```matlab

syms x; % 定义符号变量

f = sin(x) * cos(x); % 定义函数

F = int(f, x); % 求解不定积分

disp(F); % 显示结果

```

运行后，MATLAB将输出：

```

(sin(2*x))/4

```

二、求解定积分

求解定积分时，除了指定函数和积分变量外，还需要指定积分区间。`int`函数也可以用于求解定积分，但需要额外提供积分上下限。

示例3：求解定积分

假设我们需要求解函数f(x) = x^2在区间[0, 1]上的定积分。

```matlab

syms x; % 定义符号变量

f = x^2; % 定义函数

a = 0; % 积分下限

b = 1; % 积分上限

I = int(f, x, a, b); % 求解定积分

disp(I); % 显示结果

```

运行后，MATLAB将输出：

```

1/3

```

这表明f(x) = x^2在区间[0, 1]上的定积分为1/3。

三、使用数值方法求解积分

虽然`int`函数非常强大，能够处理大多数符号积分问题，但在某些情况下，特别是当函数表达式非常复杂或无法用符号表示时，数值方法可能更为适用。MATLAB提供了`integral`函数用于数值积分。

示例4：使用数值方法求解定积分

假设我们需要求解函数f(x) = exp(-x^2)在区间[0, +∞)上的定积分（这是高斯函数的一个特例，其值为√π/2）。

```matlab

f = @(x) exp(-x.^2); % 定义匿名函数

a = 0; % 积分下限

b = inf; % 积分上限

I = integral(f, a, b); % 使用数值方法求解定积分

disp(I); % 显示结果

```

运行后，MATLAB将输出一个接近√π/2的值（由于数值方法的精度限制，可能会有轻微误差）。

四、积分技巧与注意事项

1. 变量替换：在求解复杂积分时，变量替换是一个常用的技巧。虽然MATLAB能够自动处理一些简单的变量替换，但在手动处理或优化代码时，了解变量替换的原理是有帮助的。

2. 积分区间的选择：对于定积分，选择合适的积分区间非常重要。在某些情况下，通过改变积分区间可以简化积分过程或提高计算效率。

3. 数值积分的精度：使用`integral`函数进行数值积分时，可以通过设置`AbsTol`和`RelTol`参数来控制积分精度。这两个参数分别表示绝对误差容限和相对误差容限。

4. 符号积分与数值积分的比较：符号积分能够给出精确结果，但计算速度较慢且受限于符号计算的能力。数值积分虽然精度有限，但计算速度快且适用于更广泛的函数类型。

5. 多变量积分：MATLAB也支持多变量积分的求解，但相对于单变量积分来说，多变量积分的求解更加复杂且计算量更大。在实际应用中，需要根据具体问题选择合适的积分方法和工具。

6. 积分路径的选择：在求解复变函数积分时，积分路径的选择非常重要。不同的积分路径可能导致不同的积分结果。MATLAB提供了复变函数工具箱来支持这类积分的求解。

7. 优化与加速：对于需要频繁计算的积分问题，可以考虑使用MATLAB的优化工具箱来加速计算过程。例如，可以通过向量化操作、并行计算等方法来提高计算效率。

综上所述，MATLAB提供了多种方法和工具来求解积分问题。无论是符号积分还是数值积分，MATLAB都能够提供准确且高效的解决方案。在实际应用中，我们需要根据具体问题的特点选择合适的积分方法和工具来求解问题。通过不断学习和实践，我们可以更好地掌握MATLAB在积分求解中的应用技巧和方法。