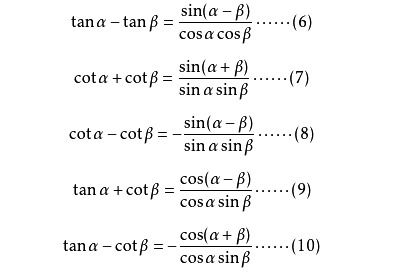余切函数图像和性质是怎样的?
余切函数的图像与性质
在数学领域中,三角函数是一类重要的函数,其中余切函数(Cotangent Function)具有独特的图像和性质。本文将详细介绍余切函数的图像及其各项性质,同时确保内容结构清晰、语言简洁明了,并合理布局关键词,以提升阅读体验和搜索引擎友好度。

余切函数的定义
余切函数,记作cot(x),是一种基本的三角函数,定义如下:对于任意一个实数x(x ≠ kπ,k为整数),都存在一个唯一的角(弧度制中等于这个实数),该角对应一个唯一的余切值cot(x)。余切函数在直角坐标系中的表达式为f(x) = cot(x)。在y = cot(x)中,以x的任一使cot(x)有意义的值与它对应的y值作为(x, y),所得到的图形称为余切函数图像,也叫余切曲线。

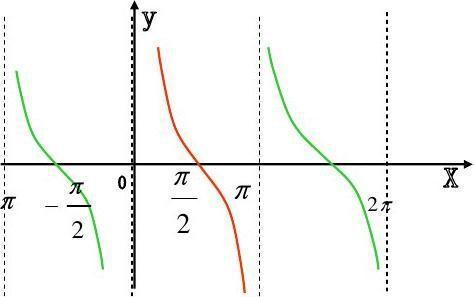
余切函数的图像
余切函数的图像由无穷多支曲线组成,这些曲线被一系列相互平行的直线x = kπ(k为整数)隔开。余切曲线在每个开区间(kπ, (k+1)π)内都有定义,且随着x的增大或减小,y值在正负无穷大之间波动。
要获得余切函数的图像,可以通过将正切函数图像进行平移和旋转操作。具体来说,将正切函数图像向左平移π/2个单位,然后将该图像绕点(x = (2k+1)π/2)旋转180度,即可得到余切函数的图像。这一过程也验证了cot(x) = tan(-x + π/2)的关系,表明余切函数和正切函数在图像上存在一定的关联性。
余切函数的性质
余切函数具有一系列重要的性质,包括定义域、值域、奇偶性、周期性、单调性等。以下是详细分析:
1. 定义域:余切函数的定义域为{x | x ≠ kπ, k ∈ Z}。由于cot(x) = cos(x)/sin(x),当x = kπ时,sin(x) = 0,导致cot(x)无意义。因此,余切函数在x = kπ处无定义。
2. 值域:余切函数的值域为实数集R。在每个开区间(kπ, (k+1)π)内,cot(x)的值从负无穷大增加到正无穷大,或从正无穷大减少到负无穷大。因此,余切函数可以取到所有实数作为函数值。
3. 奇偶性:余切函数是奇函数。根据诱导公式cot(-x) = -cot(x),可以得出余切函数关于原点对称。进一步观察可以发现,余切函数图像关于点(kπ/2, 0)(k为整数)对称,这些点也是函数的对称中心。
4. 周期性:余切函数是周期函数,周期为kπ(k为整数且k ≠ 0)。最小正周期T = π。这意味着,对于任意实数x和整数k,cot(x + kπ) = cot(x)。余切函数的周期性在图像上表现为无限重复的波形。
5. 单调性:在每个开区间(kπ, (k+1)π)(k为整数)内,余切函数是单调递减的。由于余切函数在这些区间内从正无穷大或减少到负无穷大,因此它不具有全局单调性。然而,在每个这样的开区间内,它都是单调递减的。
6. 对称性:除了上述关于点(kπ/2, 0)的对称性外,余切函数还具有中心对称性。这一性质与余切函数的图像结构紧密相关,使得函数图像在视觉上呈现出特定的美感。
7. 零点:余切函数的零点为x = π/2 + kπ(k为整数)。在这些点上,cot(x) = 0。这些零点对应于函数图像上的渐近线,即当x趋近于这些点时,y值趋近于正负无穷大。
应用与实例
余切函数在物理、工程和天文学等领域中有广泛的应用。例如,在物理中,余切函数可以用于描述某些周期性现象;在工程领域,余切函数可以用于信号处理和控制系统设计;在天文学中,余切函数可以用于计算天体位置和轨道参数。
具体实例方面,假设我们需要计算一个角度的余切值,可以使用计算器或编程语言中的三角函数库来直接求解。此外,在解决涉及余切函数的方程或不等式时,可以利用余切函数的性质和图像来简化问题。
结论
余切函数作为一种重要的三角函数,具有独特的图像和
-
 揭秘余切函数:深入探索其图像与奇妙性质新闻资讯11-09
揭秘余切函数:深入探索其图像与奇妙性质新闻资讯11-09 -
 如何绘制lnx绝对值的清晰图像教程新闻资讯10-21
如何绘制lnx绝对值的清晰图像教程新闻资讯10-21 -
 详解三角函数:sec、csc、cot 的定义与公式新闻资讯10-25
详解三角函数:sec、csc、cot 的定义与公式新闻资讯10-25 -
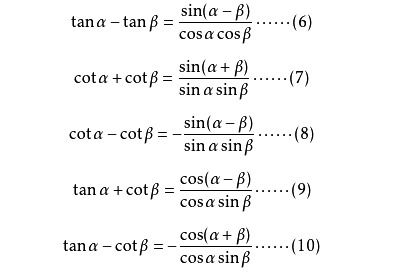 余切公式的定义是什么?新闻资讯11-09
余切公式的定义是什么?新闻资讯11-09 -
 如何在函数图像上区分并划分第一、第二、第三、第四象限?新闻资讯11-01
如何在函数图像上区分并划分第一、第二、第三、第四象限?新闻资讯11-01 -
 揭秘:函数奇偶性加减乘除判定口诀大公开!新闻资讯11-13
揭秘:函数奇偶性加减乘除判定口诀大公开!新闻资讯11-13