余切公式的定义是什么?
余切公式:探索三角学的奥秘
在数学世界中,三角学作为一门历史悠久且应用广泛的学科,承载着众多引人入胜的知识。今天,我们将一起探索三角学中的一个重要概念——余切公式。这不仅是一段关于数学公式的旅程,更是一次对逻辑思维和数学美的欣赏。

初识余切
当我们谈论直角三角形时,很容易联想到正弦、余弦和正切这三个基本三角函数。然而,余切(Cotangent)这个听起来稍显陌生的函数,同样在三角学中扮演着重要的角色。余切的定义非常简单:在直角三角形中,某锐角的相邻直角边和相对直角边的比,叫做该锐角的余切,即余切=角的邻边÷角的对边。用数学符号表示就是cot A = b/a,其中b是角的邻边,a是角的对边。
余切与正切是互为倒数的关系,用“cot+角度”来表示。例如,30°的余切表示为cot 30°,角A的余切表示为cot A。旧时用ctg A来表示余切,但现代数学中更常用cot A来表示。
余切公式的几何意义
余切公式不仅是一个数学表达式,它还承载着深刻的几何意义。在直角三角形中,余切值可以帮助我们理解角的大小与边长之间的关系。具体来说,余切值的大小反映了锐角与其相邻直角边相对于对边长度的比例关系。
为了更好地理解余切公式的几何意义,我们可以通过构造一些具体的直角三角形来观察余切值的变化。例如,在一个30°-60°-90°的直角三角形中,30°角的余切值为√3/3,而在45°-45°-90°的直角三角形中,45°角的余切值为1。通过比较这些数值,我们可以发现余切值随着锐角大小的变化而变化,这种变化关系正是余切公式的几何意义所在。
余切函数的性质
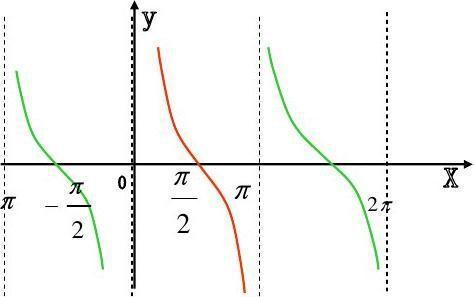
余切函数作为三角函数的一种,具有许多独特的性质。首先,余切函数的定义域是{x|x≠kπ, k∈Z},即除了整数倍的π以外的所有实数都是余切函数的定义域。这意味着在直角坐标系中,余切函数的图像是由一些隔离的分支组成的。
其次,余切函数的值域是实数集R,即余切值可以取任何实数值。由于余切函数没有最大值和最小值,因此它的图像在直角坐标系中会无限延伸。
此外,余切函数还是奇函数和周期函数。奇函数的性质意味着余切函数的图像关于原点对称;而周期函数的性质则意味着余切函数具有周期性,其最小正周期是π。在每一个开区间(kπ, (k+1)π)上,余切函数都是减函数,这使得余切函数的图像呈现出一种特有的“波浪状”。
余切公式的应用
余切公式在三角学和数学的其他分支中有着广泛的应用。首先,在解决与直角三角形相关的问题时,余切公式可以帮助我们快速找到角的度数或边长。例如,在已知一个锐角及其相邻直角边和对边的长度时,我们可以利用余切公式求出另一个锐角的度数。
其次,余切公式在三角函数的计算和推导中发挥着重要作用。通过余切公式,我们可以推导出其他三角函数的相关公式和性质。例如,我们可以利用余切公式推导出正弦定理和余弦定理等重要的三角学定理。
此外,余切公式还在物理学、工程学等自然科学领域中有着广泛的应用。例如,在物理学中,余切公式可以用于计算物体的运动轨迹和速度;在工程学中,余切公式可以用于计算结构的稳定性和强度等。
余切定理与余切公式的联系
在三角学中,余切定理是另一个与余切相关的重要概念。余切定理是关于三角形内切圆半径的定理,它表述为:某个角一半的余切等于半周长减去这个角所对的边长再除以三角形的内切圆半径。这个定理在解决与三角形内切圆相关的问题时非常有用。
余切定理与余切公式之间存在一定的联系。虽然它们的表述和应用场景不同,但它们都涉及到余切函数的概念和性质。通过余切定理和余切公式的结合使用,我们可以更全面地理解和解决与三角形和三角函数相关的问题。
探索余切公式的奥秘
余切公式不仅是一个数学工具,更是一个充满奥秘的数学世界。通过深入探索余切公式的性质和应用,我们可以发现数学中的许多美妙之处。
首先,余切公式的周期性让我们感受到了数学中的节奏和规律。每一个周期都代表着一种重复和变化,这种变化中又蕴含着一种不变和稳定。这种稳定性和变化性的结合正是数学美的体现之一。
其次,余切公式的奇偶性让我们感受到了数学中的对称和平衡。奇函数和偶函数的图像都呈现出一种特有的对称性,这种对称性不仅
-
 详解三角函数:sec、csc、cot 的定义与公式新闻资讯10-25
详解三角函数:sec、csc、cot 的定义与公式新闻资讯10-25 -
 余切函数图像和性质是怎样的?新闻资讯11-10
余切函数图像和性质是怎样的?新闻资讯11-10 -
 曲率公式的定义是什么新闻资讯10-31
曲率公式的定义是什么新闻资讯10-31 -
 斜率的定义及公式是什么新闻资讯11-13
斜率的定义及公式是什么新闻资讯11-13 -
 电容的计算公式是什么新闻资讯11-06
电容的计算公式是什么新闻资讯11-06 -
 等价无穷小公式是什么?初学者如何理解和应用这些公式?新闻资讯12-22
等价无穷小公式是什么?初学者如何理解和应用这些公式?新闻资讯12-22