详解三角函数:sec、csc、cot 的定义与公式
在探讨数学的广阔领域中,三角函数占据了举足轻重的地位,它们不仅是解析几何的基石,也在物理、工程、计算机科学等多个领域发挥着不可或缺的作用。在众多三角函数中,除了我们熟知的正弦(sin)、余弦(cos)和正切(tan)之外,还有三个同样重要的反函数——正割(sec)、余割(csc)和余切(cot)。这些函数虽然不如前三者那般直观,但在解决特定问题时却异常有用。下面,我们就来详细解析sec、csc、cot这三个三角函数的定义、基本公式及其性质。

一、定义初识
1. 正割(secant, 简称sec)
正割函数是余弦函数的倒数。对于任意角θ(θ ≠ kπ + π/2, k为整数),其正割值定义为:
\[ \sec\theta = \frac{1}{\cos\theta} \]
这里需要注意的是,当θ为π/2 + kπ(k为整数)时,cosθ=0,因此secθ无定义。
2. 余割(cosecant, 简称csc)
余割函数是正弦函数的倒数。同样地,对于任意角θ(θ ≠ kπ, k为整数),其余割值定义为:
\[ \csc\theta = \frac{1}{\sin\theta} \]
类似地,当θ为整数倍的π时,sinθ=0,因此cscθ也无定义。
3. 余切(cotangent, 简称cot)
余切函数是正切函数的倒数。对于任意角θ(θ ≠ kπ/2 + π/2, k为整数),其余切值定义为:
\[ \cot\theta = \frac{1}{\tan\theta} = \frac{\cos\theta}{\sin\theta} \]
这里,由于tanθ在θ为kπ/2 + π/2(k为整数)时无定义(因为此时sinθ=0),所以cotθ在这些点上也无定义。
二、基本公式与关系
1. 基本恒等式
除了上述定义外,sec、csc、cot之间以及与sin、cos、tan之间还存在着紧密的联系。以下是它们之间的一些基本恒等式:
\[ \sec^2\theta = 1 + \tan^2\theta \]
\[ \csc^2\theta = 1 + \cot^2\theta \]
\[ \tan\theta = \frac{\sin\theta}{\cos\theta} = \frac{1}{\cot\theta} \]
\[ \sec\theta \cdot \cos\theta = 1 \]
\[ \csc\theta \cdot \sin\theta = 1 \]
这些恒等式揭示了三角函数之间的内在联系,是推导更复杂公式和解决问题的基础。
2. 和差公式
对于sec、csc、cot的和差公式,虽然不如sin、cos、tan的和差公式那样直观,但通过它们与sin、cos、tan的关系,可以间接得到。例如,利用tan的和差公式和cot与tan的倒数关系,可以推导出cot的和差公式。不过,由于直接表达较为复杂,且在实际应用中更多是通过转换为sin、cos、tan的形式来处理,这里不再详述。
3. 倍角公式与半角公式
类似地,sec、csc、cot的倍角公式与半角公式也可以通过与sin、cos、tan的倍角公式和半角公式的联系来推导。例如,利用sin、cos的倍角公式和sec、csc的定义,可以推导出它们的倍角表达式。这些公式在处理复杂三角函数问题时非常有用。
三、应用实例
虽然sec、csc、cot在日常生活中的应用不如sin、cos、tan那样直观,但在某些特定领域,如天文学、地图制作、工程计算等,它们却扮演着重要角色。例如,在解决直角三角形问题时,如果已知一个角的正弦或余弦值,且需要求解该角的正割或余割值,就可以直接应用其定义公式进行计算。
此外,在三角恒等式的证明和化简中,sec、csc、cot也经常作为中间变量出现,帮助简化复杂的表达式或证明特定的结论。
四、结语
综上所述,正割(sec)、余割(csc)和余切(cot)作为三角函数的重要组成部分,虽然在日常应用中可能不如正弦、余弦和正切那样频繁出现,但它们在解决特定问题、推导复杂公式以及理解三角函数之间的内在联系方面发挥着不可替代的作用。通过本文的介绍,希望读者能够对这些函数有一个更全面、更深入的认识,
- 上一篇: 抖音的创作者服务中心具体在哪里可以找到?
- 下一篇: 交管12123官方电脑版快速登录入口
-
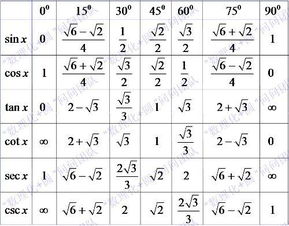 数学中cot的定义及常见应用方法新闻资讯10-24
数学中cot的定义及常见应用方法新闻资讯10-24 -
 揭秘!SEC究竟等于什么?点击即知答案!新闻资讯10-20
揭秘!SEC究竟等于什么?点击即知答案!新闻资讯10-20 -
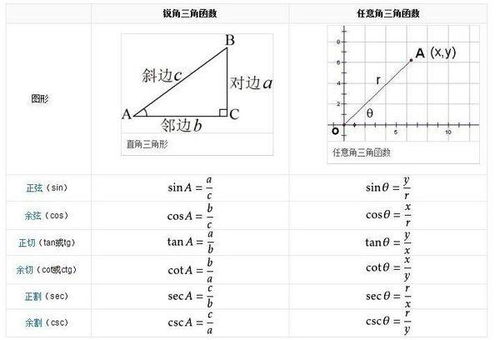 SEC的等价值是什么新闻资讯11-26
SEC的等价值是什么新闻资讯11-26 -
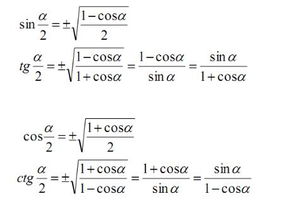 详解半角公式与二倍角公式的定义与应用新闻资讯10-18
详解半角公式与二倍角公式的定义与应用新闻资讯10-18 -
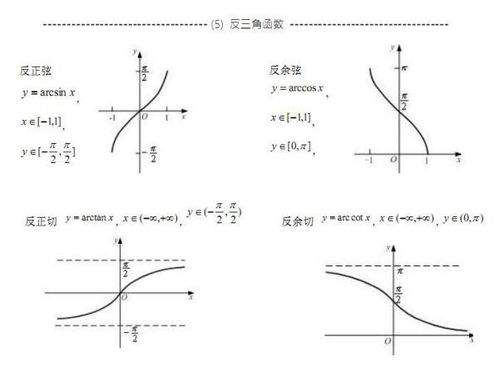 arc三角函数的导数分别是什么?新闻资讯11-22
arc三角函数的导数分别是什么?新闻资讯11-22 -
 轻松掌握:log函数求导公式详解新闻资讯11-09
轻松掌握:log函数求导公式详解新闻资讯11-09












