揭秘！SEC究竟等于什么？点击即知答案！

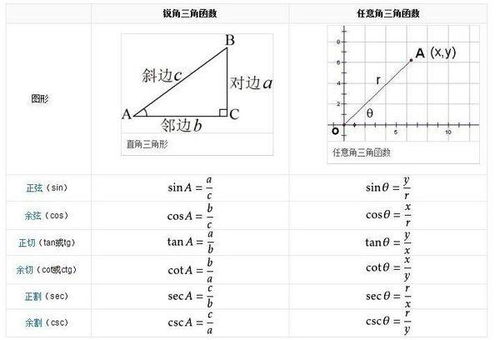
在探讨“sec等于什么”这一数学问题时，我们首先需要明确的是，sec是三角函数中的一个基本成员，全称为“secant”，意为“正割”。与正弦（sin）、余弦（cos）和正切（tan）等三角函数一样，secant函数在数学、物理及工程等多个领域都有广泛的应用。下面，我们将从定义、性质、与其他三角函数的关系、应用领域以及计算方法等方面，全面解析“sec等于什么”。

一、sec的定义

在数学中，对于任意角θ（无论角度制还是弧度制），其secant（简称sec）函数的定义为：

$$ \sec\theta = \frac{1}{\cos\theta} $$

这里，$\cos\theta$ 是θ的余弦值。简而言之，secθ是θ的余弦值的倒数。由于余弦函数的值域是$[-1, 1]$（但不包括-1和1），因此sec函数的值域是$(-\infty, -1] \cup [1, +\infty)$，即除了不存在（即余弦值为0的点，如$\theta = \frac{\pi}{2} + k\pi, k \in \mathbb{Z}$）的情况外，sec函数可以取到所有实数。

二、sec的性质

1. 周期性：与正弦、余弦和正切函数一样，sec函数也是周期函数，其周期为$2\pi$。这意味着对于任何整数k，都有$\sec(\theta + 2k\pi) = \sec\theta$。

2. 奇偶性：sec函数是偶函数，即对于任意角θ，都有$\sec(-\theta) = \sec\theta$。这一性质源于余弦函数的偶性（$\cos(-\theta) = \cos\theta$）。

3. 无穷大与无穷小：当θ趋近于$\frac{\pi}{2} + k\pi$（k为整数）时，$\cos\theta$趋近于0，因此$\sec\theta$趋近于无穷大或无穷小（取决于θ的符号）。这些点被称为sec函数的不连续点或垂直渐近线。

4. 与正切的关系：由于$\tan\theta = \frac{\sin\theta}{\cos\theta}$，我们可以推导出$\tan\theta = \sec\theta \cdot \sin\theta$，进一步说明了sec和tan之间的紧密联系。

三、sec与其他三角函数的关系

与余弦（cos）：最直接的关系，互为倒数。

与正弦（sin）：通过Pythagorean恒等式$\sin^2\theta + \cos^2\theta = 1$，可以推导出$\sin\theta = \pm \sqrt{1 - \cos^2\theta}$，进而有$\sin\theta = \pm \frac{1}{\sqrt{\sec^2\theta}}$（注意，这里需要谨慎处理符号和sec的定义域）。

与正切（tan）：如前所述，$\tan\theta = \sec\theta \cdot \sin\theta$，这反映了它们之间的乘积关系。

与余割（csc）：余割函数是正弦函数的倒数，即$\csc\theta = \frac{1}{\sin\theta}$。虽然sec与csc没有直接的等式关系，但它们都是基本三角函数的倒数，且都涉及到了倒数运算。

四、sec的应用领域

1. 三角学和几何学：在解决三角形问题、圆的性质以及更复杂的几何构造时，sec函数常作为工具出现。

2. 物理学：在力学、波动理论（如声学和光学中的波动）以及电磁学等领域，sec函数经常用于描述某些物理现象或计算相关参数。

3. 工程学：在土木工程、机械工程以及电子工程等领域，sec函数可用于计算坡度、倾斜角度、结构稳定性等，是工程师们不可或缺的数学工具。

4. 天文学：在天文观测和计算天体位置时，三角函数包括sec函数被广泛应用，以处理角度、距离和速度等参数。

五、sec的计算方法

1. 查表法：在过去，人们常常通过查阅三角函数表来获取sec等三角函数的值。

2. 计算器或软件：现代科技使得计算sec值变得异常简单，只需在计算器或数学软件中输入相应的角度或弧度值，即可直接得到结果。

3. 公式推导：对于复杂的表达式或特殊情况，可能需要通过三角恒等式、和差公式等数学工具进行推导计算。

4. 单位圆法：在直角坐标系中，以原点为圆心、半径为1的圆称为单位圆。通过在单位圆上