如何在函数图像上区分并划分第一、第二、第三、第四象限?
在数学中,函数图像是研究函数性质与变化规律的重要工具。当我们提及在函数图像上划分1234象限时,实际上是在平面直角坐标系这一背景下进行的。平面直角坐标系由两条互相垂直且交点为原点的数轴(横轴称为x轴,纵轴称为y轴)组成,它们将平面分为四个部分,即我们通常所说的第一象限、第二象限、第三象限和第四象限。以下将从多个维度深入探讨函数图像在这四个象限中的表现与特性。
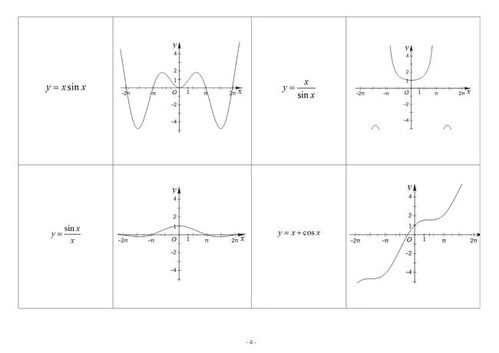
一、坐标系基础与象限定义
首先,明确坐标系的基本结构和象限的划分标准至关重要。在平面直角坐标系中,x轴的正半轴向右延伸,负半轴向左延伸;y轴的正半轴向上延伸,负半轴向下延伸。坐标系的原点(0,0)是两条坐标轴的交点。根据点的横纵坐标的正负性,平面被划分为四个区域:
第一象限:所有x坐标和y坐标都为正的点组成的区域。
第二象限:所有x坐标为负、y坐标为正的点组成的区域。
第三象限:所有x坐标和y坐标都为负的点组成的区域。
第四象限:所有x坐标为正、y坐标为负的点组成的区域。
二、函数图像在象限内的分布
不同类型的函数图像在平面直角坐标系中的表现各异,其穿越或停留在不同象限的方式也各不相同。
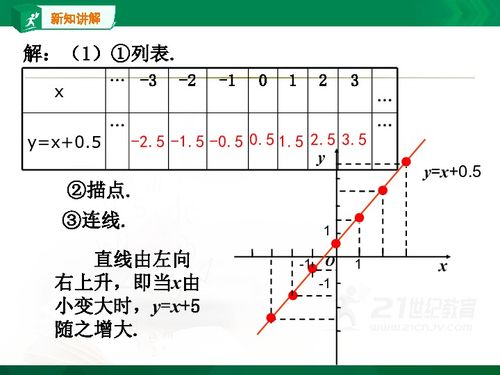
1. 线性函数
线性函数(形如y=kx+b,其中k和b为常数,k≠0)的图像是一条直线。直线的位置取决于斜率k和截距b的值。
当k>0且b>0时,直线从第三象限穿过原点进入第一象限。
当k>0且b<0时,直线从第四象限穿过原点进入第一象限。
当k<0且b>0时,直线从第二象限穿过原点进入第四象限。
当k<0且b<0时,直线从第二象限穿过第三象限。
2. 二次函数
二次函数(形如y=ax^2+bx+c,其中a≠0)的图像是一个抛物线。其开口方向、顶点位置及与坐标轴的交点决定了它在哪些象限内可能出现。
当a>0时,抛物线开口向上,可能穿过第一、第二象限(或仅在第一象限内,取决于顶点位置);若顶点在x轴下方,还可能穿过第三、四象限。
当a<0时,抛物线开口向下,可能穿过第三、四象限(或仅在第三象限内),若顶点在x轴上方,还可能穿过第一、二象限。
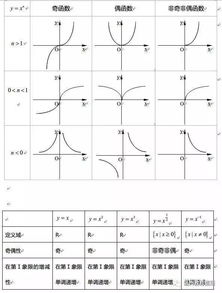
3. 指数函数与对数函数
指数函数(如y=a^x,a>0且a≠1)的图像在a>1时,始终在第一、二象限;在0
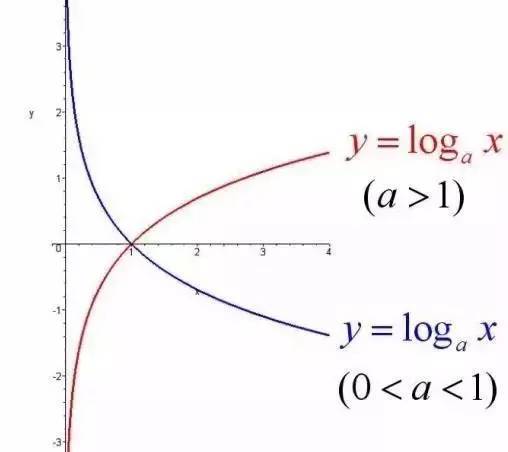
对数函数(如y=log_a(x),a>0且a≠1)的图像在a>1时,始终在第一、四象限;在0
-
 如何理解并区分象限的一、二、三、四?新闻资讯11-02
如何理解并区分象限的一、二、三、四?新闻资讯11-02 -
 掌握英文缩写艺术:'第一'、'第二'、'第三'、'第四'的优雅简写秘籍新闻资讯10-21
掌握英文缩写艺术:'第一'、'第二'、'第三'、'第四'的优雅简写秘籍新闻资讯10-21 -
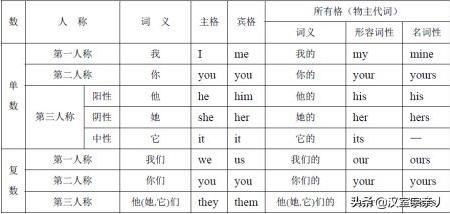 什么是第一人称、第二人称和第三人称?新闻资讯11-06
什么是第一人称、第二人称和第三人称?新闻资讯11-06 -
 PS CS6新增哪些炫酷功能?揭秘第三弹!新闻资讯12-12
PS CS6新增哪些炫酷功能?揭秘第三弹!新闻资讯12-12 -
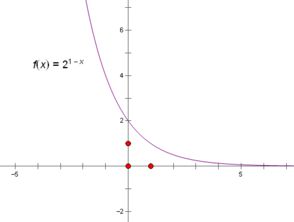 用函数画图宝绘制指数函数图像的方法新闻资讯10-27
用函数画图宝绘制指数函数图像的方法新闻资讯10-27 -
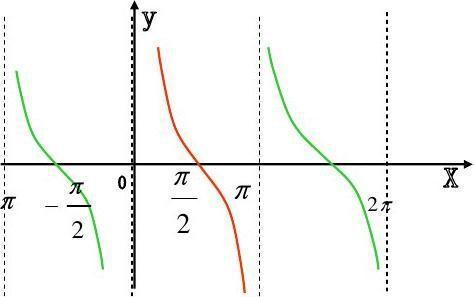 揭秘余切函数:深入探索其图像与奇妙性质新闻资讯11-09
揭秘余切函数:深入探索其图像与奇妙性质新闻资讯11-09












