扇形面积计算的三大核心公式
在数学的广阔天地里,几何学以其独特的逻辑美和空间想象力,吸引着无数学者与爱好者的目光。扇形,作为几何学中一个基础而重要的概念,不仅在理论研究中占据一席之地,更在现实生活中的应用中频繁亮相,如风扇叶片的形状、部分圆盘的区域等。探讨扇形的面积公式,我们不难发现,虽然核心公式只有一个直接用于计算扇形面积的表达式,但围绕这一核心,可以从三个不同维度深入理解其推导过程、应用场景以及与其他几何概念的关联,从而更全面地把握扇形面积公式的精髓。
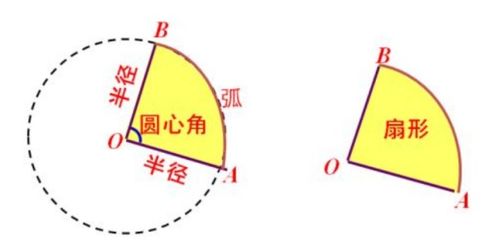
一、扇形面积公式的核心表达式
首先,我们直接给出扇形面积的核心公式:扇形面积 = (圆心角/360°) × π × 半径^2。这一公式直观地反映了扇形面积与其所在圆的面积、圆心角以及半径之间的关系。其中,圆心角决定了扇形占整个圆的比例,而半径则决定了圆(及扇形)的大小。通过这一公式,我们可以快速准确地计算出任意扇形区域的面积。

二、从推导过程看扇形面积公式的多维理解
1. 几何直观推导
从几何直观的角度出发,我们可以将圆想象成一个由无数个等宽的圆环堆叠而成的三维物体(虽然实际是二维图形,但此处的想象有助于理解)。当这些圆环被“切片”成扇形时,扇形面积就相当于这些圆环在二维平面上的投影。通过考虑圆心角占整个圆周的比例,我们可以将整个圆的面积按照这一比例分配给扇形,从而推导出扇形面积的计算公式。

2. 比例与分割
另一个理解扇形面积公式的角度是通过比例与分割。由于圆的周长是2πr(r为半径),那么圆心角所对应的弧长就是(圆心角/360°) × 2πr。进一步地,如果我们考虑一个与扇形同底等高的直角三角形(其底为扇形的弧长,高为半径),这个三角形的面积与扇形面积之间存在一定的比例关系(实际上是扇形面积的一半,但在直接推导扇形面积时并不直接使用这一关系)。然而,通过这一思路,我们可以感受到扇形面积与圆心角、半径之间的紧密联系,以及如何通过比例关系来理解复杂的几何问题。
3. 积分方法
对于有一定数学基础的学习者来说,还可以从微积分的角度理解扇形面积的推导。将扇形的弧长细分为无限多个小段,每小段可以近似看作一个直角三角形,其面积可通过底乘高除以二来计算。随着分割的无限细化,这些小三角形的面积和将趋近于扇形的真实面积。这一过程实际上是对弧长上的点进行积分,从而得到扇形面积的过程,虽然对于初学者而言可能较为抽象,但它展示了数学中“以直代曲”的思想精髓。
三、扇形面积公式的应用场景
1. 工程设计与制造
在工程设计领域,扇形面积的计算至关重要。例如,在设计风扇叶片时,需要根据风扇的转速、所需风量等因素,计算出叶片的合理面积和形状,以确保风扇的效率和性能。此时,扇形面积公式成为设计师手中的有力工具。
2. 地理学与地图制作
虽然直接的扇形面积计算在地理学和地图制作中可能不是主流,但扇形作为描述方向或视角范围的一种方式,其概念在相关领域有所体现。比如,在绘制地形图或气候分布图时,可能会用到类似扇形的区域划分来表示特定的地理特征或气候类型。
3. 经济学与统计分析
在经济学和统计分析中,扇形图作为一种常见的图表类型,用于表示数据的比例关系。尽管这里的“扇形”更多是作为一种视觉元素而非严格的几何形状,但其背后蕴含的面积概念(即各部分所占的比例)与扇形面积的计算有着异曲同工之妙。通过调整扇形的面积大小,可以直观地展示不同数据项之间的对比关系。
四、扇形面积公式与其他几何概念的关联
扇形面积的计算不仅独立存在,还与众多其他几何概念紧密相连。例如,它与圆的面积、弧长、角度等概念相互交织,共同构成了几何学的一个有机整体。此外,扇形面积的计算还涉及到比例、分数、代数运算等更广泛的数学知识,体现了数学内部不同分支之间的紧密联系和相互支撑。
综上所述,扇形面积公式虽然简洁明了,但其背后蕴含着丰富的数学思想和广泛的应用价值。从推导过程、应用场景到与其他几何概念的关联,每一个维度都为我们提供了深入理解这一公式的窗口。通过不断探索和实践,我们可以更加熟练地运用扇形面积公式解决实际问题,并在这一过程中不断加深对几何学和数学整体的理解与热爱。
- 上一篇: 高效除甲醛!这些方法让你家空气焕然一新
- 下一篇: 解锁风筝的正确拼音拼读,让童心飞扬在蓝天下!
-
 揭秘!扇形面积的三大计算公式,你掌握了吗?新闻资讯10-27
揭秘!扇形面积的三大计算公式,你掌握了吗?新闻资讯10-27 -
 如何计算扇形的面积?新闻资讯10-27
如何计算扇形的面积?新闻资讯10-27 -
 轻松学会:如何计算扇形的弧长新闻资讯11-05
轻松学会:如何计算扇形的弧长新闻资讯11-05 -
 揭秘!圆形面积的神奇计算公式,一学就会的几何奥秘新闻资讯10-23
揭秘!圆形面积的神奇计算公式,一学就会的几何奥秘新闻资讯10-23 -
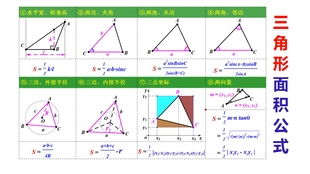 三角形面积计算公式详解新闻资讯11-25
三角形面积计算公式详解新闻资讯11-25 -
 揭秘!直角三角形面积计算的神奇公式新闻资讯10-30
揭秘!直角三角形面积计算的神奇公式新闻资讯10-30