如何计算扇形的面积?
在几何学的广阔领域中,扇形作为一种特殊的平面图形,其面积的计算不仅是理论学习的基础,也是实际应用中不可或缺的一环。扇形,顾名思义,是由圆上两条半径及它们之间的弧所围成的图形。掌握扇形面积的计算方法,不仅能帮助我们更深入地理解圆的性质,还能在工程设计、艺术设计、统计学等多个领域发挥重要作用。以下,我们就来详细探讨如何求解扇形的面积。
一、认识扇形
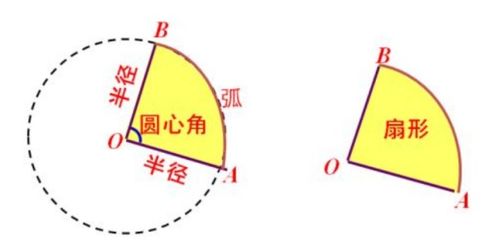
首先,我们需要明确扇形的几个关键要素:圆心角、半径和弧长。圆心角是扇形顶点在圆心处所夹的角,通常用度数或弧度来表示;半径则是从圆心到圆上任意一点的距离,它是扇形的一个重要尺寸;而弧长则是扇形边界上由圆心角对应的那段圆弧的长度。这三者之间有着紧密的联系,尤其是圆心角和弧长,它们共同决定了扇形的“大小”。

二、扇形面积的计算公式
扇形面积的计算,核心在于利用圆心角与整个圆(即圆心角为360°或2π弧度时)面积的比例关系。这里,我们主要介绍两种常用的扇形面积计算公式:

1. 公式一(基于圆心角的度数)
若扇形圆心角为n°(n为小于或等于360的正整数),半径为r,则扇形面积S的计算公式为:

\[ S = \frac{n\pi r^{2}}{360} \]
这个公式直观地体现了扇形面积与圆心角和半径之间的关系:圆心角越大,扇形面积越大;半径越长,扇形面积也越大。
2. 公式二(基于圆心角的弧度)
在弧度制下,若扇形圆心角为α(α为实数,且0≤α≤2π),半径仍为r,则扇形面积S的计算公式变为:
\[ S = \frac{1}{2} \alpha r^{2} \]
这个公式在涉及三角函数和微积分等更高级的数学运算时尤为方便,因为它直接建立了扇形面积与圆心角弧度值之间的线性关系。
三、公式的推导与理解
推导思路(基于圆心角度数公式)
我们可以将扇形视为由无数个微小的三角形(以圆心为顶点,两条相邻的半径和它们之间的一小段圆弧为边)组成。当这些三角形足够小时,它们的面积之和就近似等于扇形的面积。而每个三角形的面积可以通过其底(即弧长的一小段)和高(即半径)来计算,最终通过积分得到整个扇形的面积。但在这里,我们采用更直观的方法——比例法,即扇形面积占整个圆面积的比例等于其圆心角占整个圆周角(360°或2π弧度)的比例。
理解与应用
理解公式:无论是基于圆心角的度数还是弧度,扇形面积的计算公式都体现了扇形作为圆的一部分这一基本事实。
应用实例:
在工程设计中,计算扇形区域的面积可以帮助工程师确定材料用量或空间布局。
在统计学中,扇形图(或称饼图)常用于表示各部分在总体中所占的比例,此时扇形面积的计算就显得尤为重要。
在艺术设计中,扇形元素的应用广泛,了解其面积计算有助于设计师更精确地控制视觉效果。
四、注意事项与拓展
精确度:在实际应用中,应根据问题的具体要求选择合适的计算方法,并注意保留必要的有效数字。
单位统一:在计算扇形面积时,应确保半径和圆心角的单位一致(如都为米或都为弧度),以避免错误。
扇形与其他图形的关系:扇形与圆、三角形等图形之间有着密切的联系,通过它们之间的关系,可以推导出更多的几何性质和计算公式。
进阶学习:对于对数学有更高要求的读者,可以进一步学习微积分中的扇形面积计算方法,了解如何通过积分直接求解扇形面积,以及这种方法在更复杂图形面积计算中的应用。
总之,扇形面积的计算是几何学中的一个基础而重要的知识点。通过掌握其计算公式和推导方法,我们不仅能更好地理解和应用这一知识点,还能为后续的学习和工作打下坚实的基础。
- 上一篇: 揭秘石斛的绝妙食用法,让健康美味尽在掌握!
- 下一篇: 一键解锁!圆通95554人工服务快速接入秘籍
-
 扇形面积计算的三大核心公式新闻资讯10-19
扇形面积计算的三大核心公式新闻资讯10-19 -
 揭秘!扇形面积的三大计算公式,你掌握了吗?新闻资讯10-27
揭秘!扇形面积的三大计算公式,你掌握了吗?新闻资讯10-27 -
 轻松学会:如何计算扇形的弧长新闻资讯11-05
轻松学会:如何计算扇形的弧长新闻资讯11-05 -
 如何计算扇形的周长新闻资讯11-06
如何计算扇形的周长新闻资讯11-06 -
 怎样绘制扇形统计图?新闻资讯11-11
怎样绘制扇形统计图?新闻资讯11-11 -
 轻松学会绘制扇形统计图的方法新闻资讯11-12
轻松学会绘制扇形统计图的方法新闻资讯11-12












