轻松学会:如何计算扇形的弧长
扇形的弧长是数学中一项重要的计算,尤其在几何、物理和工程等领域有着广泛的应用。扇形是由一条弧和经过这条弧两端的两条半径所围成的图形,其弧长是指这两条半径之间的圆弧长度。为了准确计算扇形的弧长,我们需要了解几种不同的弧长公式及其适用条件。
首先,通用的弧长公式是基于圆心角和半径的关系得出的。圆心角是扇形所占圆周的角度部分,通常以度数(°)或弧度(rad)表示。假设圆心角为n度,半径为R,那么弧长L可以通过以下公式计算:
L = nπR / 180°
这个公式表明,弧长与圆心角成正比,与半径也成正比。例如,如果一个圆的半径为5厘米,扇形的圆心角为90度,那么扇形的弧长就是:
L = 90π × 5 / 180 = 2.5π ≈ 7.85厘米
另一种计算弧长的方法是直接使用弧度制。弧度制是一种与圆相关的角度度量单位,其中1弧度等于圆的弧长与半径相等的角的度数。在弧度制下,弧长L与圆心角α(以弧度为单位)和半径R的关系可以表示为:
L = R × α
这个公式简化了计算过程,特别是在涉及三角函数和微积分的应用中,弧度制更为常用。例如,如果圆心角α为π/4弧度(即45度),半径R为3厘米,那么扇形的弧长就是:
L = 3 × π/4 = 3π/4 ≈ 2.36厘米
除了上述两种基本公式,我们还可以通过扇形与整个圆的关系来推导弧长。由于一个完整的圆周长是2πR,而扇形的圆心角是360°的几分之一,因此扇形的弧长也可以是整个圆周长的几分之一。具体地,如果圆心角为n度,那么扇形的弧长L可以通过以下公式计算:
L = 2πR × n / 360°
这个公式也被称为扇形弧长的第二公式,它同样表明了弧长与圆心角和半径的关系,只是以不同的方式表示出来。例如,如果一个圆的半径为4厘米,扇形的圆心角为60度,那么扇形的弧长就是:
L = 2π × 4 × 60 / 360 = 4π/3 ≈ 4.19厘米
在实际应用中,我们需要根据具体的条件选择合适的公式进行计算。例如,在已知圆心角和半径的情况下,我们可以直接使用通用的弧长公式或弧度制公式;在已知扇形所占圆周的比例时,我们可以使用扇形弧长的第二公式。此外,我们还可以通过已知弧长和半径来求解圆心角,或者通过已知弧长和圆心角来求解半径,这些都可以通过公式变换来实现。
需要注意的是,在计算过程中,我们需要明确角度的单位是度数还是弧度,因为这会直接影响到公式的选择和计算结果的准确性。另外,对于复杂的几何图形或实际问题,我们可能需要结合多个公式和定理进行综合分析,以得出正确的结论。
除了计算弧长,扇形还涉及面积的计算。扇形的面积与圆心角和半径也有密切的关系。假设圆心角为n度,半径为R,那么扇形的面积S可以通过以下公式计算:
S = nπR² / 360°
这个公式表明,扇形的面积与圆心角成正比,与半径的平方也成正比。同样地,如果圆心角采用弧度制,那么扇形的面积可以表示为:
S = 1/2 × R² × α
这个公式简化了计算过程,特别是在处理与圆相关的几何问题时更为方便。
综上所述,扇形的弧长计算是数学中一项重要的技能,它涉及到圆心角、半径以及不同的公式和单位。通过掌握这些基本概念和公式,我们可以准确地计算扇形的弧长和面积,从而解决各种实际问题。在实际应用中,我们还需要注意公式的选择和计算过程的准确性,以确保结果的可靠性。
此外,扇形的弧长和面积计算在数学教育中也具有重要意义。通过学习和练习这些计算技能,学生可以培养逻辑思维和解决问题的能力,为未来的学习和工作打下坚实的基础。因此,在数学教育中,我们应该注重扇形的弧长和面积计算的教学和实践,帮助学生掌握这些基本技能和知识。
总之,扇形的弧长计算是数学中一个重要的组成部分,它涉及到多种公式和单位的应用。通过掌握这些概念和公式,我们可以准确地计算扇形的弧长和面积,为实际应用提供有力的支持。同时,这些计算技能在数学教育中也具有重要意义,可以帮助学生培养逻辑思维和解决问题的能力。希望本文的介绍能够帮助读者更好地理解和应用扇形的弧长计算技能。
- 上一篇: SCI期刊与SCI论文详解
- 下一篇: 邮政银行95580,轻松掌握转人工服务的秘诀!
-
 如何计算扇形的面积?新闻资讯10-27
如何计算扇形的面积?新闻资讯10-27 -
 揭秘!扇形面积的三大计算公式,你掌握了吗?新闻资讯10-27
揭秘!扇形面积的三大计算公式,你掌握了吗?新闻资讯10-27 -
 如何计算扇形的周长新闻资讯11-06
如何计算扇形的周长新闻资讯11-06 -
 轻松学会绘制扇形统计图的方法新闻资讯11-12
轻松学会绘制扇形统计图的方法新闻资讯11-12 -
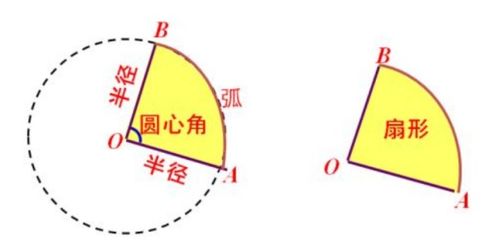 扇形面积计算的三大核心公式新闻资讯10-19
扇形面积计算的三大核心公式新闻资讯10-19 -
 如何在Word中创建扇形统计图新闻资讯12-05
如何在Word中创建扇形统计图新闻资讯12-05