如何理解正交矩阵的定义及其性质?
在数学的浩瀚宇宙中,矩阵作为连接代数与几何、线性方程组求解、乃至量子物理等领域的桥梁,扮演着举足轻重的角色。而在这一系列的矩阵变换与特性中,正交矩阵以其独特的性质脱颖而出,成为了数学研究与工程应用中一颗璀璨的明珠。那么,什么是正交矩阵?让我们一同揭开它神秘的面纱,探索其背后的奥秘与魅力。

正交矩阵的初步印象
想象一下,在二维或三维空间中,我们常使用坐标系来描述点的位置、向量的方向和长度。当我们说一个变换(比如旋转、反射)是“正交”的时,实际上是指这个变换在保持长度不变(即“保距”)的同时,还保留了向量间的直角关系。将这些概念抽象到数学领域,正交矩阵便是这样一类特殊的矩阵,它们在执行线性变换时,能够确保这些几何特性不被破坏。

定义揭秘
正式地,一个n×n的实矩阵Q被称为正交矩阵,如果它满足条件:Q的转置矩阵Q^T与其自身的乘积等于单位矩阵I,即Q^T * Q = I。同样地,这也意味着Q乘以Q的转置也等于单位矩阵,即Q * Q^T = I。这一性质确保了正交矩阵在进行线性变换时,不会改变向量的长度(模),且任意两个经过变换后的向量之间的夹角保持不变,这正是“正交”一词所蕴含的几何直观。
几何视角的阐释
从几何角度看,正交矩阵对应的线性变换可视为一种“刚体变换”。刚体变换是指在变换过程中,物体内部任意两点之间的距离保持不变的变换,它可以是平移、旋转或两者的组合,但不包括缩放、扭曲等非刚体变形。因此,正交矩阵描述的是一种既不拉伸也不压缩空间,仅仅通过旋转和/或反射来改变对象方向或镜像的变换。
性质探索
1. 行列式为±1:由于正交矩阵保持向量长度不变,其行列式必然为1(当变换保持空间定向时)或-1(当变换改变空间定向,如镜面反射时)。这一性质使得正交矩阵在几何上具有重要意义,能够明确地区分旋转变换与包含反射的变换。
2. 逆矩阵的简便性:正交矩阵的一个非常实用的性质是其逆矩阵等于其转置矩阵,即Q^-1 = Q^T。这意味着求解涉及正交矩阵的线性方程组变得异常简单,无需复杂的逆矩阵计算过程。
3. 保持内积:正交变换还保留了向量间的内积,即对于任意两个向量x和y,它们在变换前后的内积相同。这一性质在信号处理、图像处理等领域有着广泛的应用,如保证信号或图像的能量在变换过程中不变。
4. 稳定性:由于正交变换不会引入新的数值误差(除了有限的计算机精度限制),因此它们被广泛应用于数值算法中,以保证计算结果的稳定性和准确性。
应用领域概览
正交矩阵及其性质在众多领域中展现出了强大的应用潜力。在信号处理中,快速傅里叶变换(FFT)的核心思想就是利用正交矩阵的特性来高效地实现频域与时域之间的转换。在图形学和计算机视觉中,正交变换常被用于旋转、缩放等图像处理操作,以保持图像的几何结构不被破坏。此外,在量子力学、统计学、最优化问题求解等领域,正交矩阵也扮演着至关重要的角色。
结语
正交矩阵,以其独特的性质和在各个领域中的广泛应用,成为了数学与工程界不可或缺的工具。它们不仅是线性代数理论的瑰宝,更是连接现实世界与数学抽象世界的桥梁。通过对正交矩阵的深入学习,我们不仅能够领略到数学之美,更能洞察到其在解决实际问题中的巨大威力。希望本文能够激发你对正交矩阵乃至整个数学世界的好奇心与探索欲,让你在知识的海洋中扬帆远航,发现更多未知的奥秘。
-
 揭秘正交矩阵:四大精妙判定法,轻松解锁矩阵世界奥秘新闻资讯10-30
揭秘正交矩阵:四大精妙判定法,轻松解锁矩阵世界奥秘新闻资讯10-30 -
 揭秘正交矩阵:线性代数中的神秘变换大师新闻资讯11-01
揭秘正交矩阵:线性代数中的神秘变换大师新闻资讯11-01 -
 如何轻松求解矩阵的逆?新闻资讯11-08
如何轻松求解矩阵的逆?新闻资讯11-08 -
 矩阵乘法的定义与运算方法新闻资讯11-22
矩阵乘法的定义与运算方法新闻资讯11-22 -
 线性代数基础:范德蒙德行列式详解与计算方法新闻资讯11-23
线性代数基础:范德蒙德行列式详解与计算方法新闻资讯11-23 -
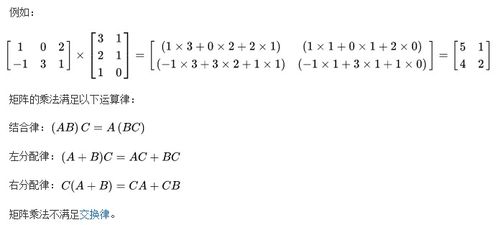 矩阵的乘法运算是怎么进行的?新闻资讯11-17
矩阵的乘法运算是怎么进行的?新闻资讯11-17