圆锥表面积的计算方法
当我们探索几何世界的奇妙时,圆锥这一立体图形以其独特的形状和广泛的应用,总能吸引无数好奇的目光。想象一下,从冰淇淋甜筒的可爱外形到宏伟建筑的屋顶设计,圆锥的身影无处不在,它不仅是自然界与人工造物中的常客,更是数学与工程学领域的重要研究对象。今天,就让我们一起揭开圆锥神秘面纱的一角,深入探讨一个既基础又迷人的话题——圆锥的表面积是什么。

圆锥的基本构造
首先,让我们简要回顾一下圆锥的基本构造。圆锥由一个圆形底面和一个顶点不在底面圆心上方的侧面围成。底面是一个完整的圆,而侧面则是一个曲面,它逐渐从底面的边缘收缩至顶点,形成一个连续的、无棱角的几何体。这种结构赋予了圆锥独特的稳定性和美学价值。

表面积的定义
表面积,简而言之,就是一个物体外部所有面的面积之和。对于圆锥而言,它包含两个主要部分:底面的面积和侧面的面积。要计算圆锥的总表面积,我们需要将这两部分的面积相加。

底面的面积
圆锥的底面是一个圆,其面积的计算相对直接。根据圆的面积公式:面积 = π × 半径²(其中π是一个常数,约等于3.14159),我们只需知道底面圆的半径长度,就能轻松计算出底面的面积。
侧面的面积
相比之下,圆锥侧面的面积计算稍显复杂,因为它涉及到的是一个曲面而非平面。但幸运的是,通过数学家的智慧,我们找到了一个简洁的公式来求解。
圆锥侧面的展开图是一个扇形,这个扇形的弧长等于圆锥底面的周长(即2πr),而扇形的半径则等于圆锥的母线长。母线是连接圆锥顶点和底面圆周上任意一点的线段。
因此,圆锥侧面的面积可以通过扇形面积的公式来计算:扇形面积 = (1/2) × 弧长 × 半径。将弧长替换为2πr,半径替换为圆锥的母线长l,我们得到圆锥侧面面积的公式:面积 = (1/2) × 2πr × l = πrl。
圆锥的总表面积
现在,我们已经知道了圆锥底面和侧面的面积计算公式,接下来就是将它们相加,得到圆锥的总表面积。即:
圆锥的总表面积 = 底面的面积 + 侧面的面积
= π × 半径² + π × 半径 × 母线长
= πr² + πrl
这个公式简洁而优美,它揭示了圆锥表面积与其几何参数(半径和母线长)之间的直接关系。
实际应用与意义
了解圆锥的表面积不仅是对数学知识的一次探索,更有着广泛的实际应用价值。在建筑设计领域,设计师需要根据建筑物的尺寸和形状来计算所需材料的数量,而圆锥屋顶的设计就离不开对其表面积的精确计算。此外,在制造业中,生产圆锥形状的产品(如冰淇淋筒、漏斗等)时,同样需要精确掌握其表面积,以便合理安排生产计划和控制成本。
结语
综上所述,圆锥的表面积是通过结合底面圆的面积和侧面扇形的面积计算得出的。这一计算过程不仅加深了我们对圆锥这一几何体的理解,还展示了数学在解决实际问题中的强大力量。无论是对于学习几何的初学者,还是从事相关领域工作的专业人士来说,掌握圆锥表面积的计算方法都是一项不可或缺的技能。希望今天的分享能够激发你对圆锥乃至整个几何世界更深层次的兴趣和探索欲望。
-
 揭秘!圆锥表面积的神奇计算公式,一看就懂!新闻资讯11-01
揭秘!圆锥表面积的神奇计算公式,一看就懂!新闻资讯11-01 -
 圆台侧面积计算公式详解新闻资讯11-23
圆台侧面积计算公式详解新闻资讯11-23 -
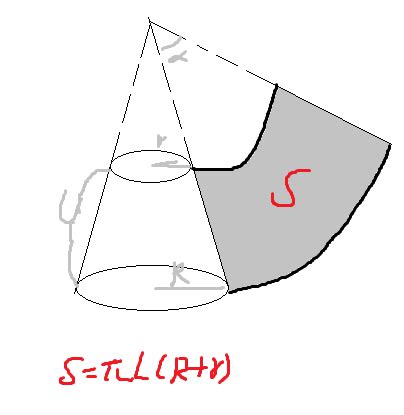 揭秘!圆台侧面积计算公式大公开,你了解多少?新闻资讯10-25
揭秘!圆台侧面积计算公式大公开,你了解多少?新闻资讯10-25 -
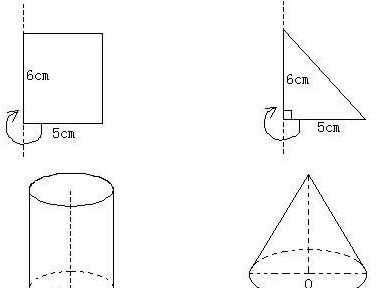 圆锥体积的计算公式是什么新闻资讯11-22
圆锥体积的计算公式是什么新闻资讯11-22 -
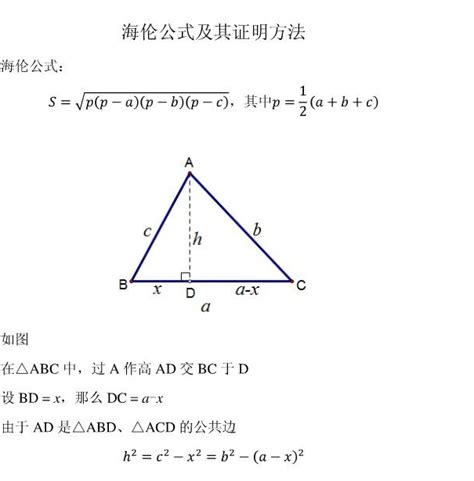 轻松学会:直角三角形面积的计算方法新闻资讯10-30
轻松学会:直角三角形面积的计算方法新闻资讯10-30 -
 揭秘圆柱体表面积的计算方法新闻资讯11-22
揭秘圆柱体表面积的计算方法新闻资讯11-22












